贝叶斯分类器
天气预报中70%降水概率怎么来的?
就是在历史统计数据中跟当天的天气状态差不多的天数中有70下雨,则可判断当天下雨的概率为70%。
贝叶斯分类器的分类原理:
通过某对象的先验概率,利用贝叶斯公式计算出其后验概率,即该对象属于某一类的概率,选择具有最大后验概率的类作为该对象所属的类。
机器学习算法中,有种依据 概率原则 进行分类的 朴素贝叶斯算法
正如气象学家预测天气一样,朴素贝叶斯算法就是应用先前事件的有关数据来估计未来事件发生的概率 。
即预测某个输入属于某一个类型的概率,大于阈值,则分到该分类下。
理解朴素贝叶斯 (Naive Bayes)
邮箱系统中垃圾邮件检测机制,如果发现垃圾邮件就会放到垃圾站:
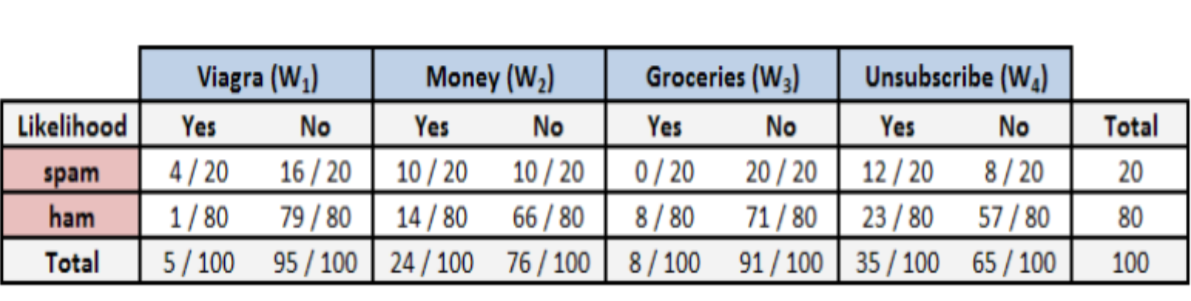
下图 spam(垃圾邮件)占数量(20%),正常邮件占80%,而Viagra占5%,求Viagra是垃圾邮件的概率?
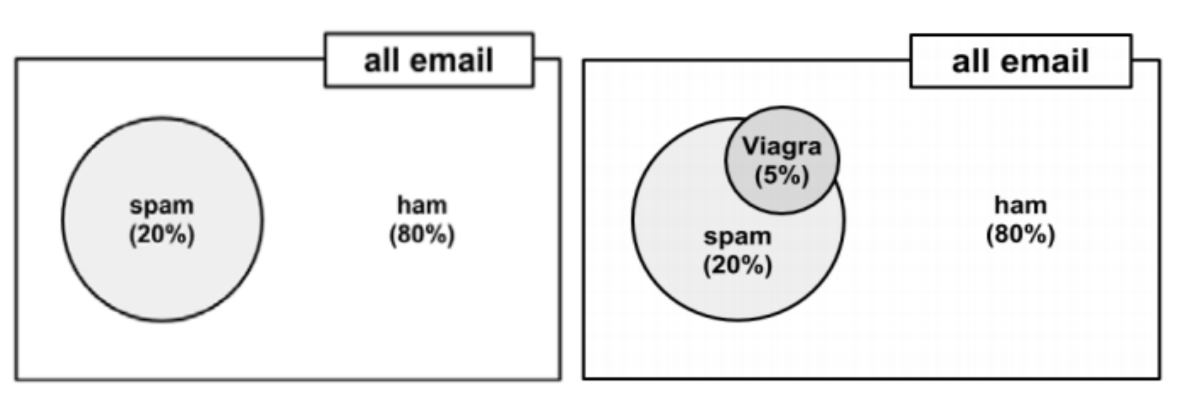
如果 我们知道P(垃圾邮件)和P(Viagra)是 相互独立 的,则容易计算P(垃圾邮件&Viagra),即这两个事件同时发生的概率: 20%*5%=1%
独立事件我们可以简单的应用这个方法计算,但是在实际中,P(垃圾邮件)和P(Viagra)更可能是 高度相关的 ,即包含某些词确实更大可能是垃圾邮件,因此上述计算是不正确的,我们需要一个精确的公式来描述这两个事件之间的关系:
假设有事件A与事件B:
A和B一起发生的概率 A ∩ B = P(B | A)P(A) = P(A | B)P(B)
那么容易推导出在 事件B发生情况下,事件A发生的概率为 : P(A | B) = A ∩ B / P(B) = P(B | A)P(A) / P(B)
所以 基于贝叶斯定理的条件概率为:
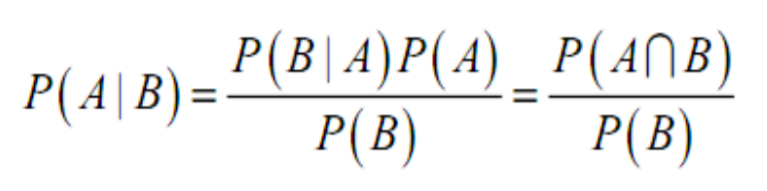
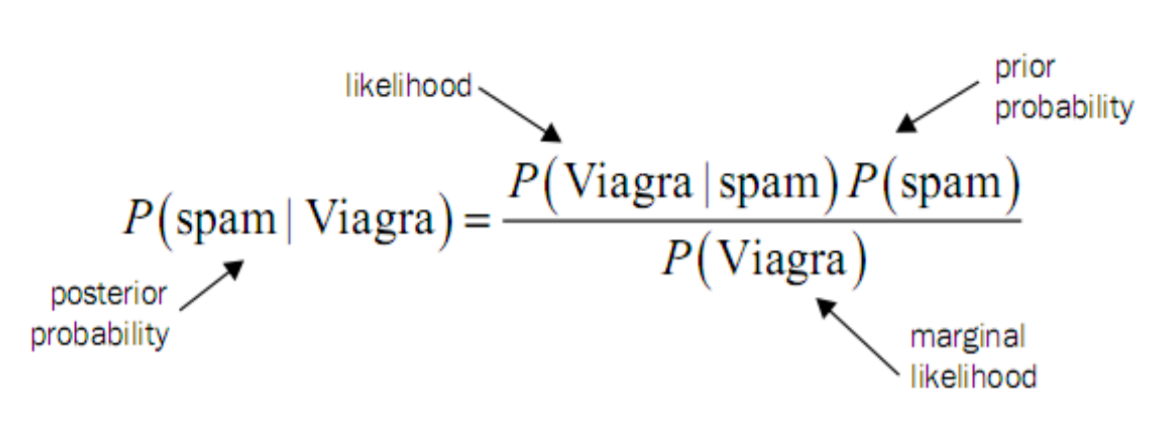
对于我们垃圾邮件来说:
计算贝叶斯定理中每一个组成部分的概率,我们必须构造一个频率表 :
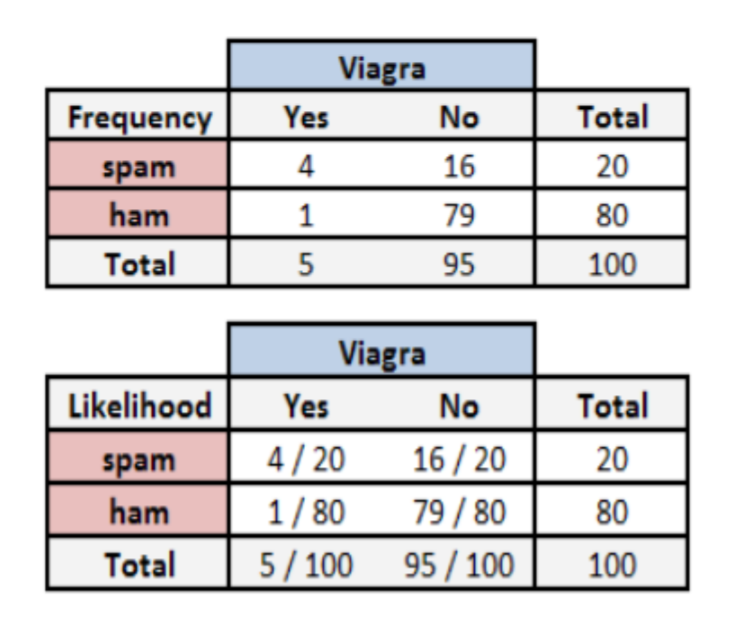
P(垃圾邮件|Viagra)= P(Viagra|垃圾邮件)*P(垃圾邮件)/P(Viagra) = (4/20)*(20/100)/(5/100) = 0.8 = P( Viagra ) ∩ P(垃圾邮件)
因此,如果电子邮件含有单词Viagra,那么该电子邮件是垃圾邮件的概率为80%。所以,任何含有单词Viagra的消息都需要被过滤掉。
当有额外更多的特征是,这一概念如何被使用 ?
在邮件中同时出现 W1、W4两个词,并且同时没有出现W2、W3时,求这封邮件是垃圾邮件的概率, 利用贝叶斯公式我们得到概率如下:
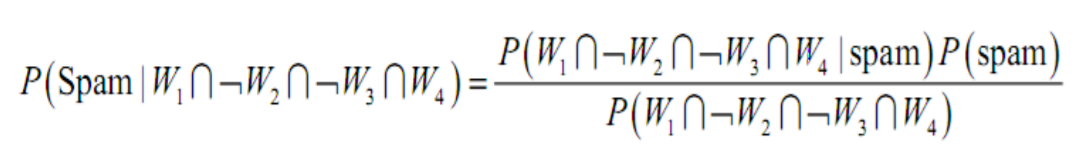
这时求 P( W1 ∩ 非W2 ∩ 非W3 ∩ W4 ) 又涉及到了条件概率的问题,这时为了降低计算复杂度,我们就假设这四个部分是相互独立的,于是该表达式就可以化简为:
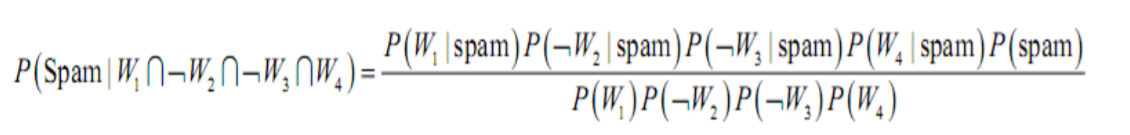
这种化简属于词袋模型: 一篇文章打乱等价于一堆词
所以垃圾邮件的总似然为:
(4/20)*(10/20)*(20/20)*(12/20)*(20/100) / (5/100)*(76/100)*(91/100)*(35/100) = 85.7%
由上可得 贝叶斯分类不需要迭代
使用场景: 适合文本分类
问题:
如果是这封邮件同时包含了这4个单词的邮件呢?
我们可以计算垃圾邮件的似然如下: (4/20)*(10/20)*(0/20)*(12/20)*(20/100) / (5/100)*(24/100)*(8/100)*(35/100) = 0
为什么变成了0呢?
问题出在Groceries这个单词,Groceries出现次数为0,所以单词Grogeries有效抵消或否决了所有其他的证据。
那怎么解决呢?
去掉Groceries这个词? 不行这样影响了数据
只好给Groceries加上一个很小的数例如1,让它不是0,但是这样对其他的数就不公平 , 所以也同时给其他的数加上1。
拉普拉斯估计
拉普拉斯估计本质上是给频率表中的 每个计数加上一个较小的数,这样就保证了 每一类中每个特征发生概率非零。
通常情况下,拉普拉斯估计中加上的数值设定为1,这样就保证每一类特征的组合至少在数据中出现一次。
然后,我们得到垃圾邮件的似然为:
(5/24)*(11/24)*(1/24)*(13/24)*(24/108) / (7/108)*(26/108)*(10/108)*(37/108) = 80%
这表明该消息是垃圾邮件的概率为80%
R语言例子:
数据:
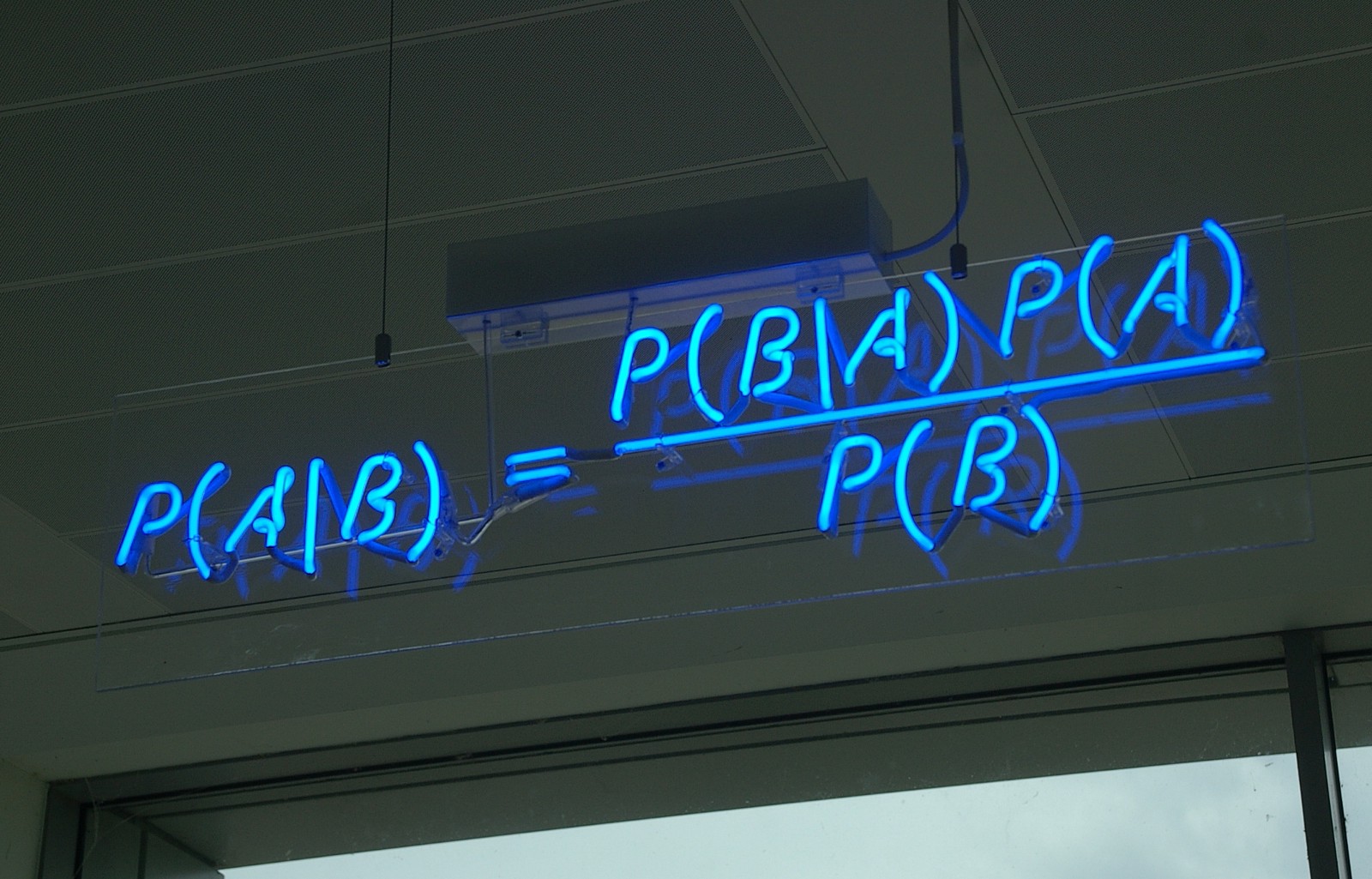
代码:
sms_raw <- read.csv("sms_spam.csv", stringsAsFactors=FALSE)
str(sms_raw)
sms_raw$type <- factor(sms_raw$type)
str(sms_raw$type)
table(sms_raw$type)
library(tm)
sms_corpus <- Corpus(VectorSource(sms_raw$text))
print(sms_corpus)
inspect(sms_corpus[1:3])
corpus_clean <- tm_map(sms_corpus, removeNumbers)
corpus_clean <- tm_map(corpus_clean, removePunctuation)
corpus_clean <- tm_map(corpus_clean, removeWords, stopwords())
corpus_clean <- tm_map(corpus_clean, stripWhitespace)
corpus_clean <- tm_map(corpus_clean, tolower)
corpus_clean <- tm_map(corpus_clean, content_transformer(tolower))
corpus_clean <- tm_map(corpus_clean, removeWords, stopwords())
corpus_clean <- tm_map(corpus_clean, stripWhitespace)
corpus_clean <- tm_map(corpus_clean, PlainTextDocument)
inspect(corpus_clean[1:3])
#给定tm语料库,创建一个稀疏矩阵要用到下述命令:
sms_dtm <- DocumentTermMatrix(corpus_clean)
#75%训练数据集和25%测试数据集
sms_raw_train <- sms_raw[1:4169,]
sms_raw_test <- sms_raw[4170:5559,]
#文档单词矩阵也分开:
sms_dtm_train <- sms_dtm[1:4169,]
sms_dtm_test <- sms_dtm[4170:5559,]
#语料库也分开:
sms_corpus_train <- corpus_clean[1:4169]
sms_corpus_test <- corpus_clean[4170:5559]
prop.table(table(sms_raw_train$type))
prop.table(table(sms_raw_test$type))
library(wordcloud)
wordcloud(sms_corpus_train, min.freq=40, random.order=FALSE)
spam <- subset(sms_raw_train, type="spam")
ham <- subset(sms_raw_train, type="ham")
wordcloud(spam$text, max.words=40, scale=c(3,0.5))
wordcloud(ham$text, max.words=40, scale=c(3,0.5))
inspect(spam[1:3,"text"])
findFreqTerms(sms_dtm_train, 5)
sms_dict <- findFreqTerms(sms_dtm_train, 5)
sms_train <- DocumentTermMatrix(sms_corpus_train, list(dictionary=sms_dict))
sms_test <- DocumentTermMatrix(sms_corpus_test, list(dictionary=sms_dict))
convert_counts <- function(x){
x <- ifelse(x>0, 1, 0)
x <- factor(x, levels=c(0,1), labels=c("NO","YES"))
return(x)
}
sms_train <- apply(sms_train, MARGIN=2, convert_counts)
sms_test <- apply(sms_test, MARGIN=2, convert_counts)
library(e1071)
sms_classifier <- naiveBayes(sms_train, sms_raw_train$type)
sms_test_pred <- predict(sms_classifier, sms_test)
library(gmodels)
CrossTable(sms_test_pred, sms_raw_test$type, prop.chisq = FALSE, prop.t = FALSE, dnn=c('predicted','actual'))
sms_classifier <- naiveBayes(sms_train, sms_raw_train$type, laplace=1)
sms_test_pred2 <- predict(sms_classifier, sms_test)
CrossTable(sms_test_pred2, sms_raw_test$type, prop.chisq = FALSE, prop.t = FALSE, dnn=c('predicted','actual'))