Scikit-Learn — Python机器学习模块 - 独伫小桥风卷袖

scikit-learn机器学习库

Scikit-Learn是基于python的机器学习模块

Scikit-Learn中的机器学习算法非常丰富，包括SVM，决策树，GBDT，KNN等等，可以根据问题的类型选择合适的模型

官网： http://scikit-learn.org/

Scikit-learn Algorithm Cheat-Sheet :

使用机器学习库对音乐分类的例子：

数据集(音乐转成特征工程)

算法使用（scikit-learn中的logistic regression）

期望结果（输入一首歌,可以对输入的歌曲进行分类）

额外支持模块（需要额外安装安装dateutil->six->pyparsing->pytz->matplotlib）

安装Python2.7 , 与下面依赖模块，需要按下面顺序安装：

1，安装VCForPython27.msi
./pip install wheel
./pip install d:/numpy-1.9.2+mkl-cp27-none-win_amd64.whl
./pip install d:/scipy-0.16.0-cp27-none-win_amd64.whl
./pip install d:/scikit_learn-0.16.1-cp27-none-win_amd64.whl
./pip install d:/python_dateutil-2.4.2-py2.py3-none-any.whl
./pip install d:/six-1.9.0-py2.py3-none-any.whl
./pip install d:/pyparsing-2.0.3-py2-none-any.whl
./pip install d:/pytz-2015.4-py2.py3-none-any.whl
./pip install d:/matplotlib-1.4.3-cp27-none-win_amd64.whl

wheel 为软件包安装工具，.whl 文件为本地安装包

1、音乐数据（音乐转成特征工程）

分类型存在文件夹中

以先把一个 wma文件 (只能是wma) 读入python,然后绘制它的频谱图 , （spectrogram）来看看是什么样的 jazz

# coding:utf-8

from scipy import fft
from scipy.io import wavfile
from matplotlib.pyplot import specgram
import matplotlib.pyplot as plt # 取别名

plt.figure(figsize=(10, 4),dpi=80)  #设置画布大小
(sample_rate, X) = wavfile.read("D:/genres/jazz/converted/jazz.00000.au.wav")
# sample_rate : 采样率，即对音乐采样的损失率
# X : Y轴的高，这里代表音乐的某一时刻的各个频率
print sample_rate, X.shape
specgram(X, Fs=sample_rate, xextent=(0,30))  #xextent ： x轴范围
plt.xlabel("time")
plt.ylabel("frequency")

plt.grid(True, linestyle='-', color='0.75')
plt.savefig("D:/genres/jazz.00000.au.wav.png", bbox_inches="tight") #保存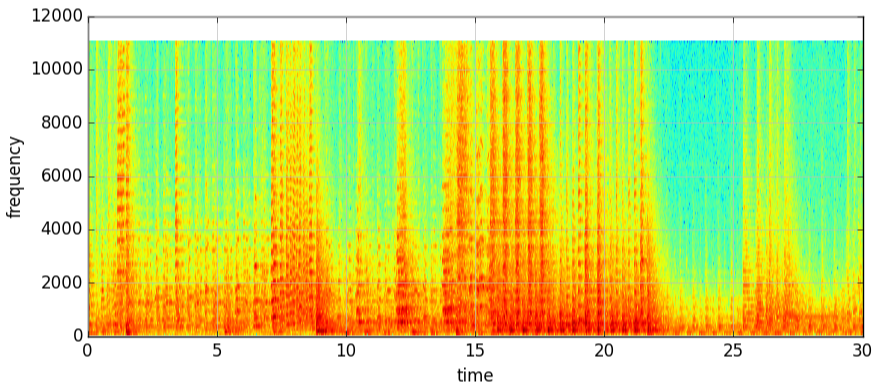

我们也可以把每一种的音乐都抽一些出来打印频谱图以便比较：

def plotSpec(g,n):
    sample_rate, X = wavfile.read("D:/genres/"+g+"/converted/"+g+"."+n+".au.wav")
    specgram(X, Fs=sample_rate, xextent=(0,30))
    plt.title(g+"_"+n[-1])

plt.figure(num=None, figsize=(18, 9), dpi=80, facecolor='w', edgecolor='k')  
plt.subplot(6,3,1);plotSpec("classical","00001");plt.subplot(6,3,2);plotSpec("classical","00002")
plt.subplot(6,3,3);plotSpec("classical","00003");plt.subplot(6,3,4);plotSpec("jazz","00001")
plt.subplot(6,3,5);plotSpec("jazz","00002");plt.subplot(6,3,6);plotSpec("jazz","00003")
plt.subplot(6,3,7);plotSpec("country","00001");plt.subplot(6,3,8);plotSpec("country","00002")
plt.subplot(6,3,9);plotSpec("country","00003");plt.subplot(6,3,10);plotSpec("pop","00001")
plt.subplot(6,3,11);plotSpec("pop","00002");plt.subplot(6,3,12);plotSpec("pop","00003")
plt.subplot(6,3,13);plotSpec("rock","00001");plt.subplot(6,3,14);plotSpec("rock","00002")
plt.subplot(6,3,15);plotSpec("rock","00003");plt.subplot(6,3,16);plotSpec("metal","00001")
plt.subplot(6,3,17);plotSpec("metal","00002");plt.subplot(6,3,18);plotSpec("metal","00003")
plt.tight_layout(pad=0.4, w_pad=0, h_pad=1.0)
plt.savefig("D:/genres/compare.au.wav.png", bbox_inches="tight")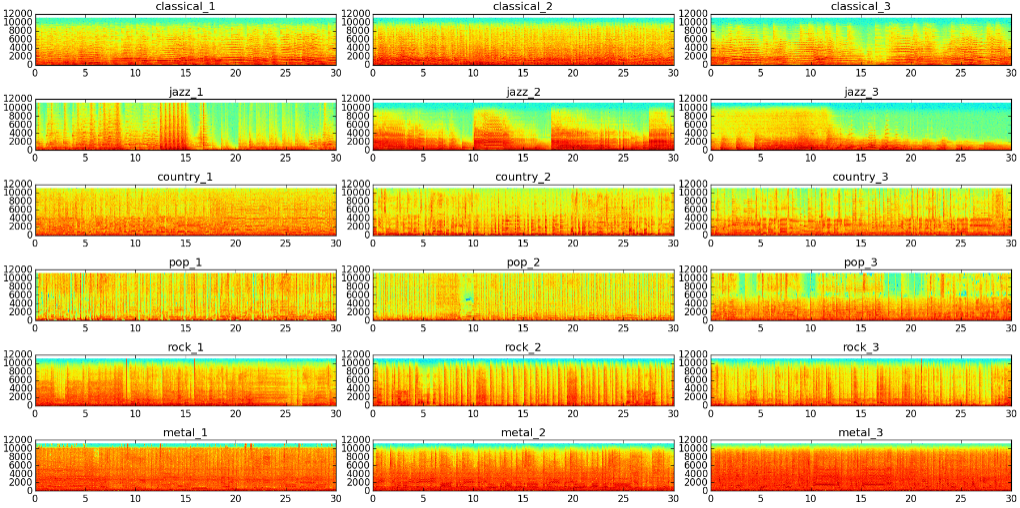

上面这种图都是以时间为角度观察频率，但是实际中每个音乐的时间长度都不一样，这样就不好比较，我们这时就可以放弃以时间为角度，即损失时间维度，来用另外一个角度看待音乐文件：

    什么是时域？？？
        股票的走势、人的身高、汽车的轨迹都会随着时间发生改变。
        这种以时间作为参照来观察动态世界的方法我们称其为时域分析
    什么是频域？？？
        频域(frequency domain)是描述信号在频率方面特性时用到的一种坐标系。用线性代数的语言就是装着正弦函数的空间。
        频域最重要的性质是：它不是真实的，而是一个数学构造。
        正弦波是频域中唯一存在的波形，这是频域中最重要的规则，即正弦波是对频域的描述，因为时域中的任何波形都可用正弦波合成。

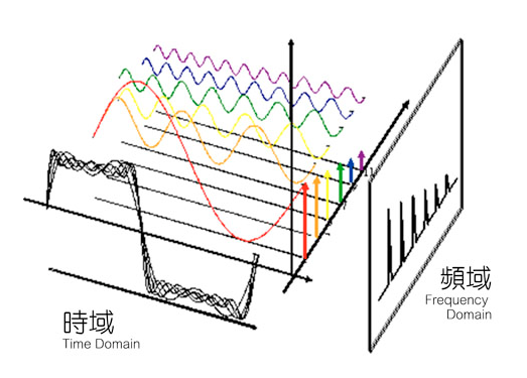
上图就是把从时域角度（看到的是各种频率交合在一起，曲线的走势是由整体决定的），而从频域角度的话，看到X轴上的各个频率，而因为没有了时间维度，所以只能看到单个频率的振幅，下面的傅里叶变换就是完成时域到频域的转换：

傅里叶变换（Fourier Transformation）

对于一个信号来说，信号强度随时间的变化规律就是时域特性，信号是由哪些单一频率的信号合成的就是频域特性。

时域分析与频域分析是对信号的两个观察面。

时域分析是以时间轴为坐标表示动态信号的关系；

频域分析是把信号变为以频率轴为坐标表示出来。

一般来说，时域的表示较为形象与直观，频域分析则更为简练，剖析问题更为深刻和方便。

贯穿时域与频域的方法之一，就是传说中的叶变换(Fourier Transformation)。

傅里叶原理表明：任何连续测量的时序或信号，都可以表示为不同频率的正弦波信号的无限叠加。

利用sox工具生成3个单一频率的文件，看看这个变换是怎么样的：

生成音乐文件 cmd执行：

C:\sox-14-4-2\sox.exe --null -r 22050 d:\sine_a.wav synth 0.2 sine 400
C:\sox-14-4-2\sox.exe --null -r 22050 d:\sine_b.wav synth 0.2 sine 3000
C:\sox-14-4-2\sox.exe --combine mix --volume 1 sine_b.wav --volume 0.5 sine_a.wav sine_mix.wav

python代码： fft() : Fast Fourier Transformation 快速傅里叶变换

# 快速傅里叶变换
# FFT是一种数据处理技巧,它可以把time domain上的数据,例如一个音频,拆成一堆基准频率,然后投射到frequency domain上
# 为了理解FFT,我们可以先生成三个音频文件
plt.figure(num=None, figsize=(12, 8), dpi=80, facecolor='w', edgecolor='k') 
plt.subplot(3,2,1)
sample_rate, a = wavfile.read("d:/sine_a.wav")
specgram(a, Fs=sample_rate, xextent=(0,30))
plt.xlabel("time")
plt.ylabel("frequency")
plt.title("400 HZ sine wave")
plt.subplot(3,2,2)
fft_a = abs(fft(a))
specgram(fft_a)
plt.xlabel("frequency")
plt.ylabel("amplitude")
plt.title("FFT of 400 HZ sine wave")
plt.subplot(3,2,3)
sample_rate, b = wavfile.read("d:/sine_b.wav")
specgram(b, Fs=sample_rate, xextent=(0,30))
plt.xlabel("time")
plt.ylabel("frequency")
plt.title("3000 HZ sine wave")
plt.subplot(3,2,4)
fft_b = abs(fft(b))
specgram(fft_b)
plt.xlabel("frequency")
plt.ylabel("amplitude")
plt.title("FFT of 3000 HZ sine wave")
plt.subplot(3,2,5)
sample_rate, c = wavfile.read("d:/sine_mix.wav")
specgram(c, Fs=sample_rate, xextent=(0,30))
plt.xlabel("time")
plt.ylabel("frequency")
plt.title("Mixed sine wave")
plt.subplot(3,2,6)
fft_c = abs(fft(c))
specgram(fft_c)
plt.xlabel("frequency")
plt.ylabel("amplitude")
plt.title("FFT of mixed sine wave")
plt.tight_layout(pad=0.4, w_pad=0, h_pad=1.0)
plt.savefig("D:/compare.sina.wave.png", bbox_inches="tight")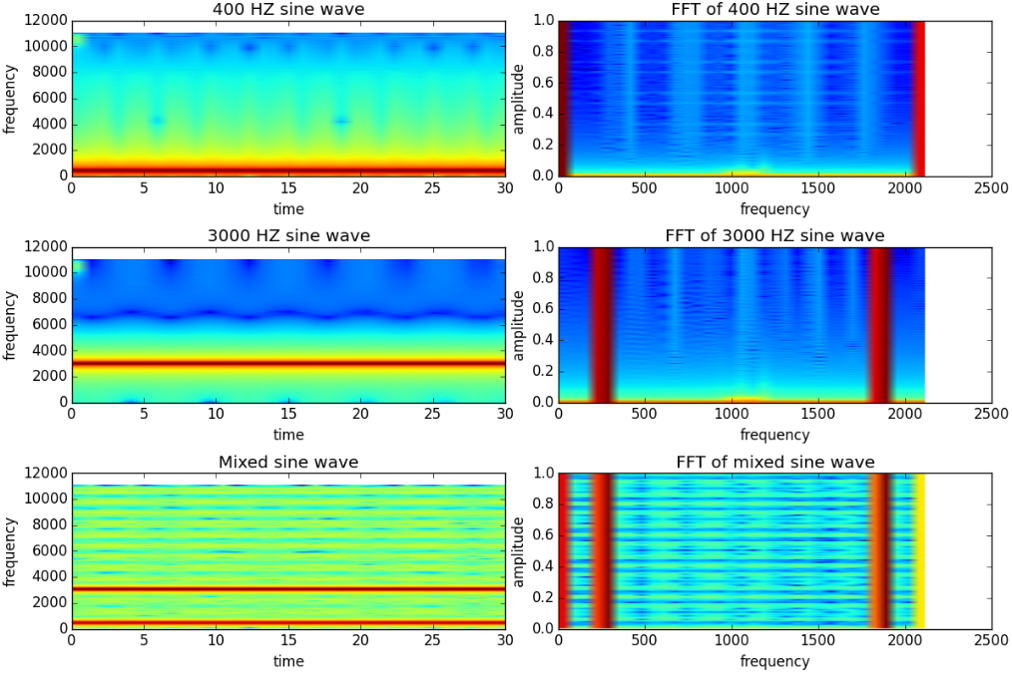

由于是单一频率，可以看到左图中为横着的直线（频率不随着时间变化），右图为竖着的直线，这里是这个频率的振幅，没有时间维度，只能看到音乐在一段时间内变换的范围。

对单首音乐进行傅里叶变换变换

可以把time domain上的数据,例如一个音频,拆成一堆基准频率,然后投射到frequency domain上

plt.figure(num=None, figsize=(9, 6), dpi=80, facecolor='w', edgecolor='k') 
sample_rate, X = wavfile.read("D:/genres/jazz/converted/jazz.00000.au.wav")
plt.subplot(2,1,1)
specgram(X, Fs=sample_rate, xextent=(0,30))
plt.xlabel("time")
plt.ylabel("frequency")
plt.subplot(2,1,2)
fft_X = abs(fft(X))  # fft() 傅里叶变换
specgram(fft_X)
plt.xlabel("frequency")
plt.ylabel("amplitude")
plt.tight_layout(pad=0.4, w_pad=0, h_pad=1.0)
plt.savefig("D:/genres/jazz.00000.au.wav.fft.png", bbox_inches="tight")

2、用逻辑回归分类

上面把音乐转成了特征工程，可以输入计算机了，这里使用逻辑回归来分类：

逻辑回归其实就是多元线性回归，只是线性回归的结果范围是负无穷到正无穷，而逻辑回归是 0到1之间，也是逻辑回归对线性回归做了归一化

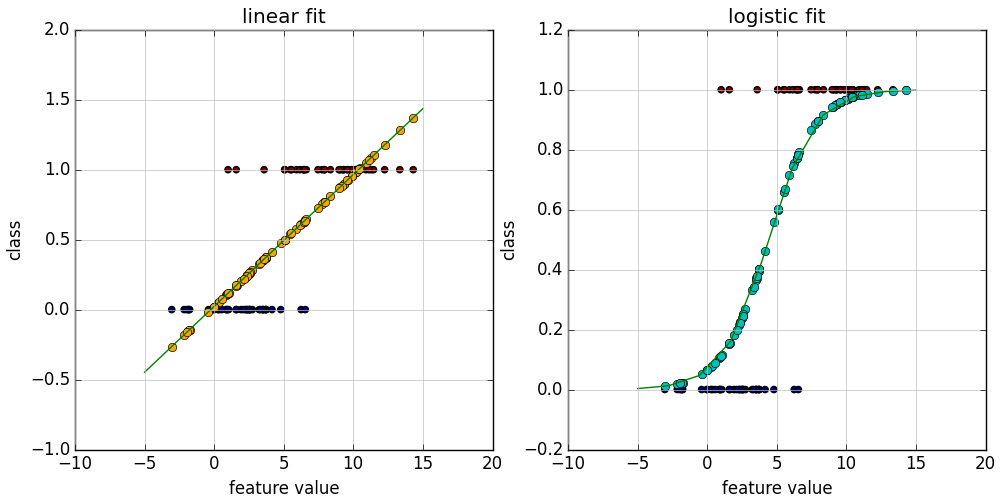
0~0.5为负值，0.5~1为正值，也就是逻辑回归是做 二分类 的，那如何做到多分类呢？

其实可以分解为做多个二分类，即对每个分类号都进行一次计算，求出该输入数据属于在这个分类的概率（二分类：是这个分类，不是这个分类），这样求出属于每个分类的概率，其中最大概率的分类为这个输入数据的分类。

这个案例流程

["classical", "jazz", "country", "pop", "rock", "metal"]

通过傅里叶变换将以上6类里面所有原始wav格式音乐文件转换为特征,并取前1000个特征,存入文件以便后续训练使用

读入以上6类特征向量数据作为训练集

使用sklearn包中LogisticRegression的fit方法计算出分类模型

读入黑豹乐队歌曲”无地自容”并进行傅里叶变换同样取前1000维作为特征向量

调用模型的predict方法对音乐进行分类,结果分为rock即摇滚类

# coding:utf-8

import numpy as np
from sklearn import linear_model, datasets
import matplotlib.pyplot as plt
from scipy.stats import norm
from scipy import fft
from scipy.io import wavfile

准备音乐数据：读取并傅里叶变换每首音乐

def create_fft(g,n):
    rad="d:/genres/"+g+"/converted/"+g+"."+str(n).zfill(5)+".au.wav"
    sample_rate, X = wavfile.read(rad)
    fft_features = abs(fft(X)[:1000])
    sad="d:/trainset/"+g+"."+str(n).zfill(5)+ ".fft" #保存
    np.save(sad, fft_features)
    
#-------creat fft--------------
 
genre_list = ["classical", "jazz", "country", "pop", "rock", "metal"]
for g in genre_list:
    for n in range(100):
        create_fft(g,n) #读取并傅里叶变换每首音乐

读取傅叶里变换后的文件，并指定分类号，作为训练数据加载到numpy ：

genre_list = ["classical", "jazz", "country", "pop", "rock", "metal"]
X=[]
Y=[]
for g in genre_list:
    for n in range(100):
        rad="d:/trainset/"+g+"."+str(n).zfill(5)+ ".fft"+".npy"
        fft_features = np.load(rad)
        X.append(fft_features)
        Y.append(genre_list.index(g))

X=np.array(X) # 数据
Y=np.array(Y) # 分类号

使用LogisticRegression训练出模型：

#------train logistic classifier-------------- 
from sklearn.linear_model import LogisticRegression
logclf = LogisticRegression()  #逻辑回归
logclf.fit(X, Y) #训练
# predictYlogistic=map(lambda x:logclf.predict(x)[0],testX)

使用模型预测黑豹乐队歌曲”无地自容” 属于哪个类别：

sample_rate, test = wavfile.read("d:/trainset/sample/heibao-wudizirong-remix.wav") #只能是单音道
# sample_rate, test = wavfile.read("d:/genres/metal/converted/metal.00080.au.wav")
testdata_fft_features = abs(fft(test))[:1000]
print sample_rate, testdata_fft_features, len(testdata_fft_features)
print logclf.predict(testdata_fft_features)[0]

独伫小桥风卷袖

邓超

Scikit-Learn — Python机器学习模块

添加新评论