逻辑回归
首先 ： 逻辑回归是一种 线性 有监督 分类 模型
何为线性？
逻辑回归本质就是多元线性回归，只是线性回归的结果范围是 负无穷到正无穷 ， 而逻辑回归是 0到1之间，也是逻辑回归对线性回归做了 归一化。
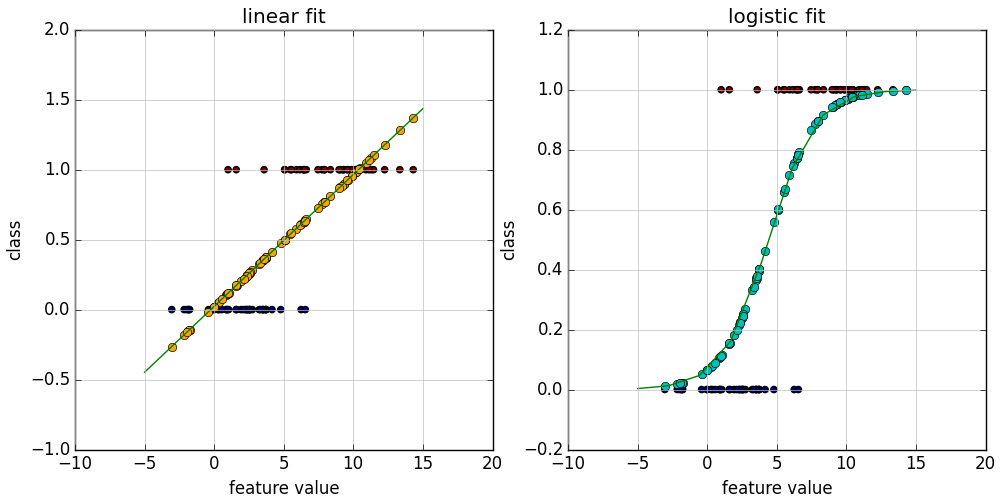
逻辑回归值在 0到1之间，0~0.5为负值，0.5~1为正值，也就是逻辑回归是做 二分类 的，那如何做到多分类呢？
其实可以分解为做多个二分类，即对每个分类号都进行一次计算，求出该输入数据属于在这个分类的概率（二分类：是这个分类，不是这个分类），这样求出属于每个分类的概率，其中最大概率的分类为这个输入数据的分类。
何为有监督？
机器学习中分为 有监督机器学习 和 无监督机器学习 ：
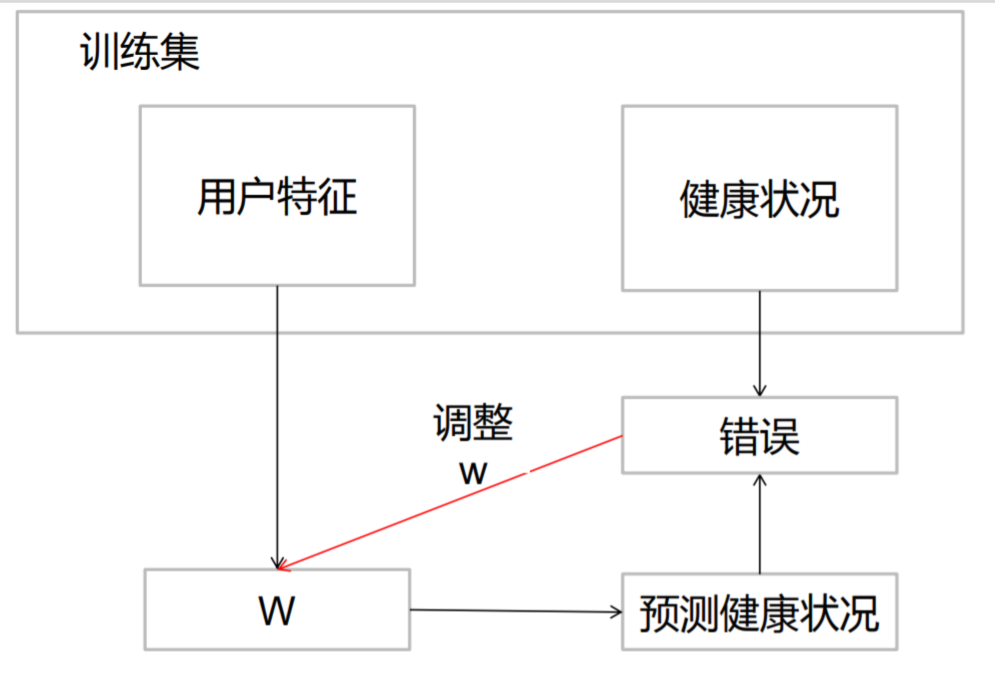
有监督其实就是 有训练集 ， 即 既有X也有Y , 有Y则可以根据Y调整模型。
无监督同理就是 只有X没有Y , 比如聚类，推荐中 就是 只给定 X，求出哪些X属于一类。
即分类中用来分类的训练数据中，是要人为的给定分类，并在训练中根据正确的分类号调整模型，使之达到最优解。
综上可得
逻辑回归是一种用于分类的模型，就相当于 y=f(x)，表明输入与输出（类别）的关系
最常见问题有如医生治病时的望、闻、问、切， 之后判定病人是否生病或生了什么病，
其中的望闻问切就是输入，即特征数据，
判断是否生病就相当于获取因变量y，即分类结果。
二分类：要么A类 要么B类
比如人的身体状况为2中：1.健康；2生病
健康的可能性是1，生病的可能性就是0
健康的可能性是0.8，生病的可能性是0.2
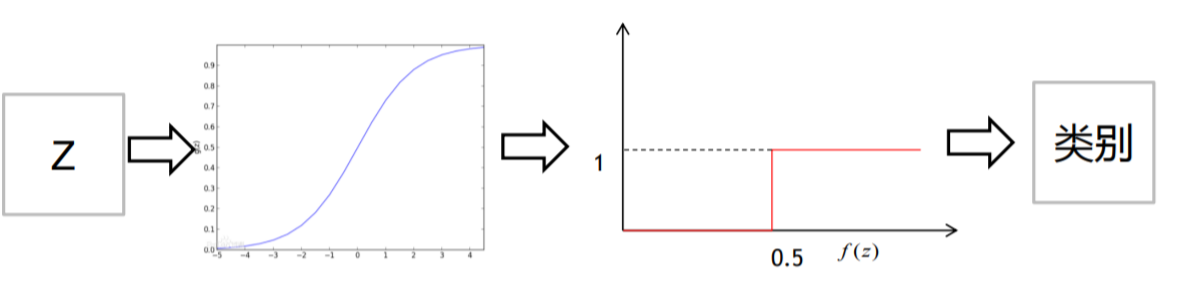
逻辑回归预测过程：
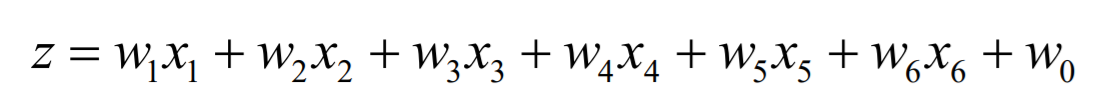
根据影响结果的维度构建多元线性方程，而方程的的代入数据求解由MLlib完成， 然后得到方程，在对方程的Y做归一化 减少到 0~1之间
那 如何归一化呢 ？ 就是如下公式
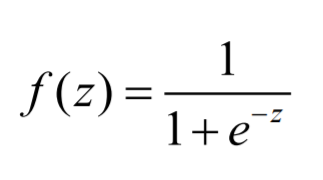
对多元线性回归方程做了归一化之后，就是如下图：
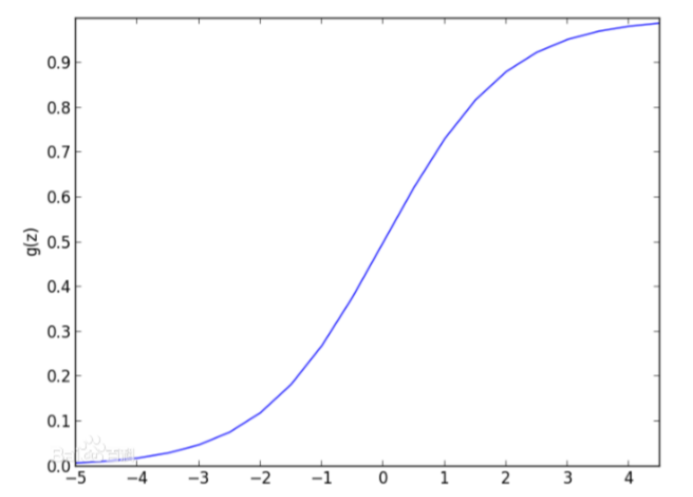
而逻辑回归又会对归一化之后的值 做二分类 （0~0.5为一类，0.5~1为另一类）：
代码：
数据：
1 1:57 2:0 3:0 4:5 5:3 6:5
1 1:56 2:1 3:0 4:3 5:4 6:3
1 1:27 2:0 3:0 4:4 5:3 6:4
1 1:46 2:0 3:0 4:3 5:2 6:4
1 1:75 2:1 3:0 4:3 5:3 6:2
1 1:19 2:1 3:0 4:4 5:4 6:4
1 1:49 2:0 3:0 4:4 5:3 6:3
1 1:25 2:1 3:0 4:3 5:5 6:4
........... LogisticRegressionWithLBFGS() : 拟牛顿法
object LogisticRegression1 {
def main(args: Array[String]) {
val conf = new SparkConf().setAppName("spark").setMaster("local[3]")
val sc = new SparkContext(conf)
val inputData: RDD[LabeledPoint] = MLUtils.loadLibSVMFile(sc, "./SparkMLlib/健康状况训练集.txt")
val splits = inputData.randomSplit(Array(0.7, 0.3), seed = 1L) // 划分训练集与测试集， 设置seed参数可以使每次随机划分的数据一样
val (trainingData, testData) = (splits(0), splits(1))
val lr = new LogisticRegressionWithLBFGS() // LogisticRegressionWithLBFGS
val model = lr.run(trainingData) // 训练得模型
val result = testData.map { point =>
Math.abs( point.label - model.predict(point.features) ) // 正确值与预测值相减
}
println("正确率=" + (1.0 - result.mean())) // result.mean() 平均值即错误值
println(model.weights.toArray.mkString(" ")) //输出w
println(model.intercept) // 输出截距
}
}结果：
根据需求的变通 去除固定阈值0.5
癌症病人的判断？ 两种错误情况
假如病人是癌症：判断成不是癌症
假如病人是非癌症： 判断是癌症
明显第一种情况是不能接受的，这样就可以将阈值降低，虽然整体的错误率变大了，但是规避了一些不能接受的风险
clearThreshold() ：
object LogisticRegression4 {
def main(args: Array[String]) {
val conf = new SparkConf().setAppName("spark").setMaster("local[3]")
val sc = new SparkContext(conf)
val inputData = MLUtils.loadLibSVMFile(sc, "健康状况训练集.txt")
val splits = inputData.randomSplit(Array(0.7, 0.3))
val (trainingData, testData) = (splits(0), splits(1))
val lr = new LogisticRegressionWithLBFGS()
lr.setIntercept(true)
val model = lr.run(trainingData).clearThreshold() //去除阈值
val errorRate = testData.map{ p=>
val score = model.predict(p.features)
// 癌症病人宁愿判断出得癌症也别错过一个得癌症的病人
val result = score>0.4 match {case true => 1 ; case false => 0} //自己判断是否是癌症
Math.abs(result-p.label)
}.mean()
println(1-errorRate)
}
}那是怎么样求解W的呢？
逻辑回归是有监督的：
即根据求出的模型带入源数据，看求出的结果与正确结果比较，使之误差达到最小，而求得w的最优解。
添加截距 W0 :
将 Z 放入带入 y的归一化公式 ， 而分类的阈值为 0.5 ：
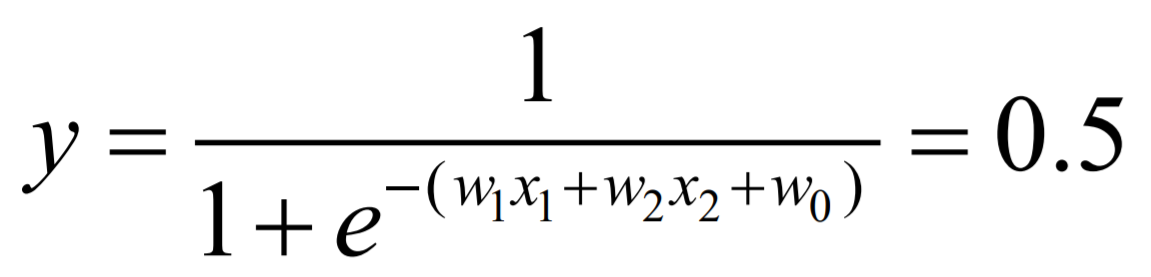
即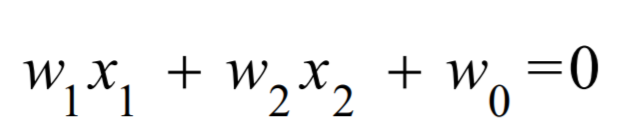 
， 也就是 ：
那我们画出 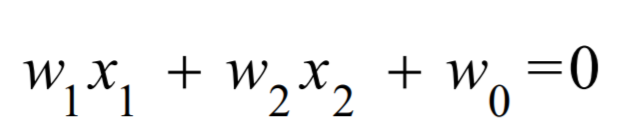的图：
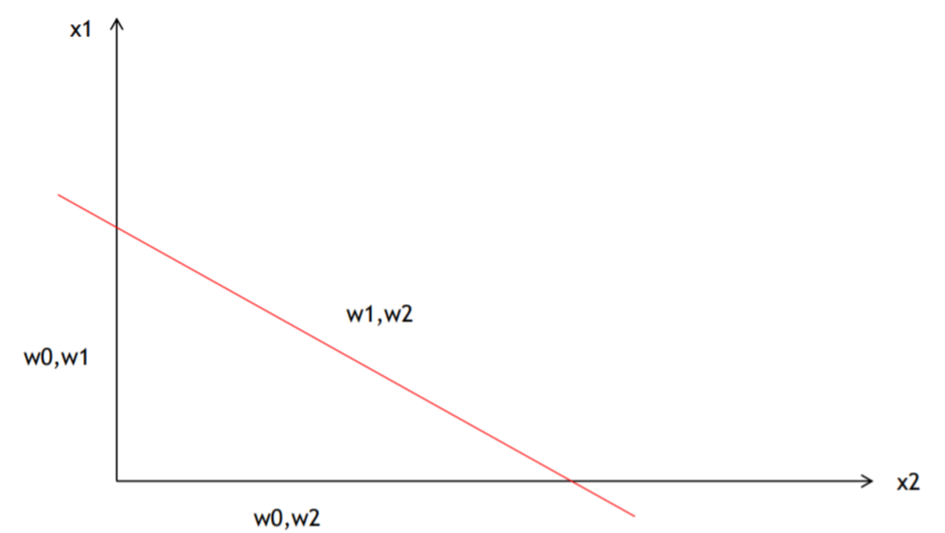
看图可得，右上部分与左下部分的方程值是 互为正负的 ， 也就是 线把两个分类的数据给分开了：
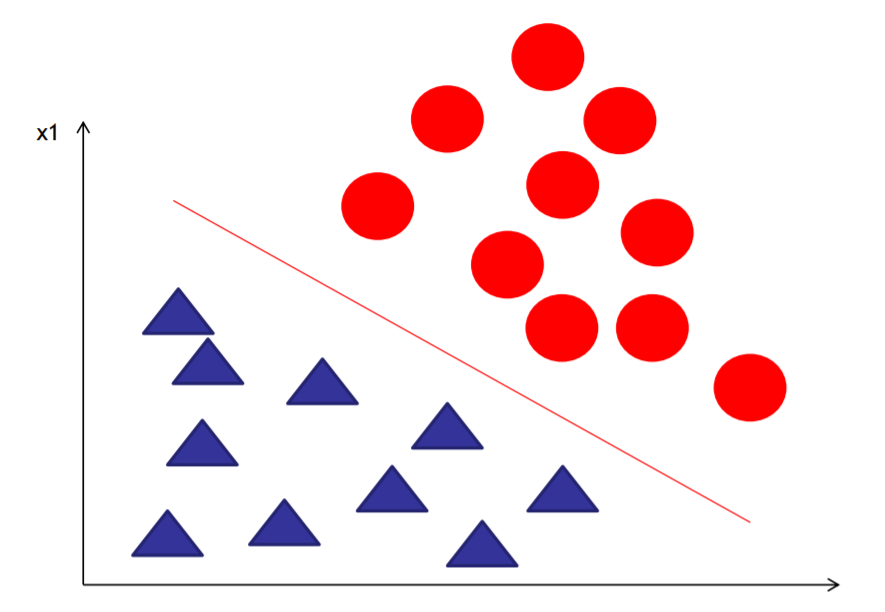
而由 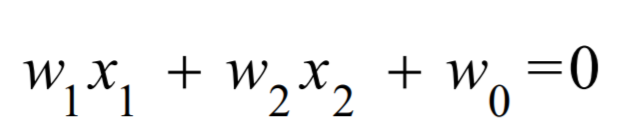可得，当 W0 为 0 时，直线是过原点的，如下图：
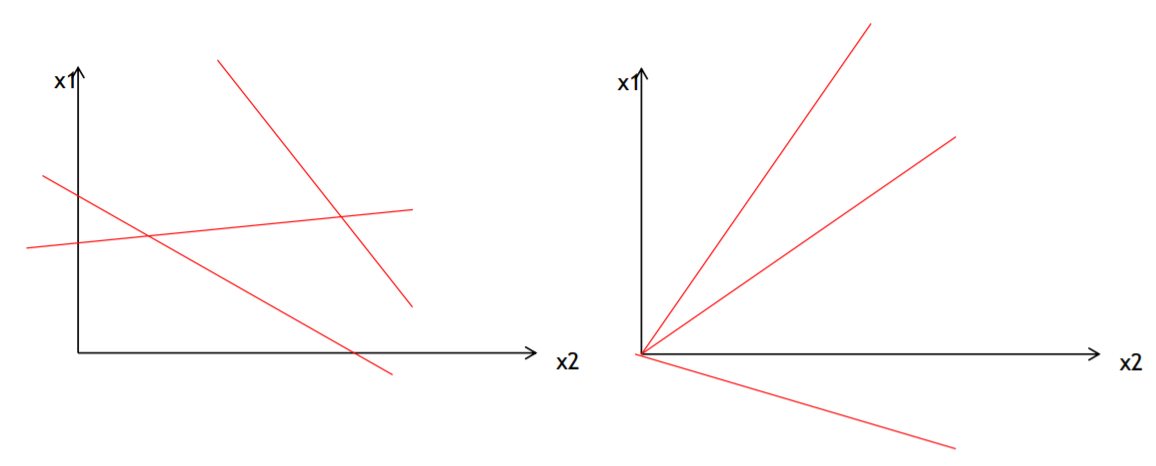
那 有w0 还是 无w0 好呢？ 有w0好，因为如果没有w0，直线就会原点，但是有很多情况的需要分类的点，是过原点的直线无法切分的，如下图：
object LogisticRegression2 {
def main(args: Array[String]) {
val conf = new SparkConf().setAppName("spark").setMaster("local[3]")
val sc = new SparkContext(conf)
val inputData: RDD[LabeledPoint] = MLUtils.loadLibSVMFile(sc, "w0测试数据.txt")
val splits = inputData.randomSplit(Array(0.7, 0.3))
val (trainingData, testData) = (splits(0), splits(1))
val lr = new LogisticRegressionWithLBFGS()
// 设置要有W0
lr.setIntercept(true)
val model=lr.run(trainingData)
val result=testData.map{point=>Math.abs(point.label-model.predict(point.features)) }
println("正确率="+(1.0-result.mean()))
println(model.weights.toArray.mkString(" "))
println(model.intercept)
}
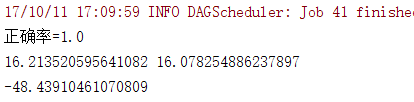
}注释 lr.setIntercept(true) 结果为：
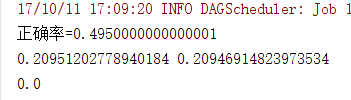
添加截距后结果为：
线性不可分：
一种特殊情况，线性不可分：
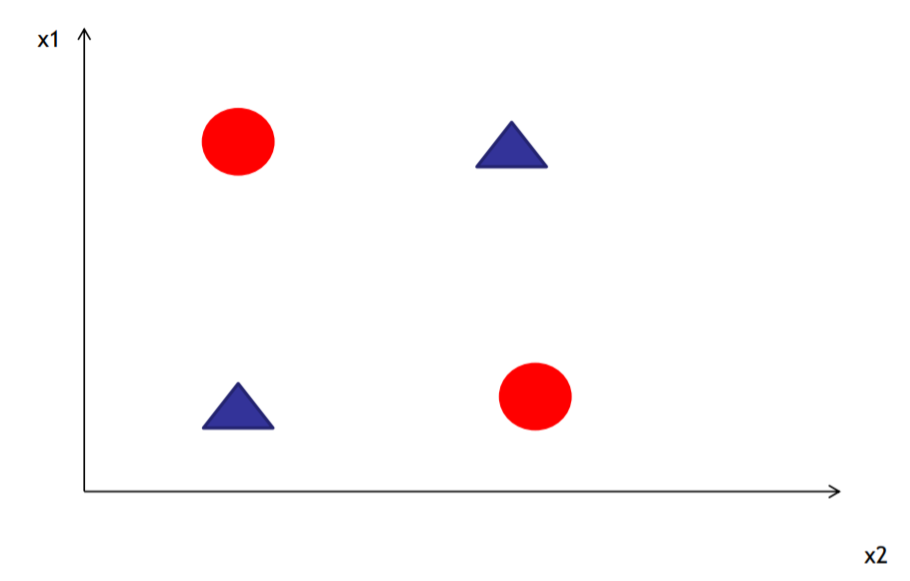
这时候一种解决方案：映射至高维 ， 即增加维度：
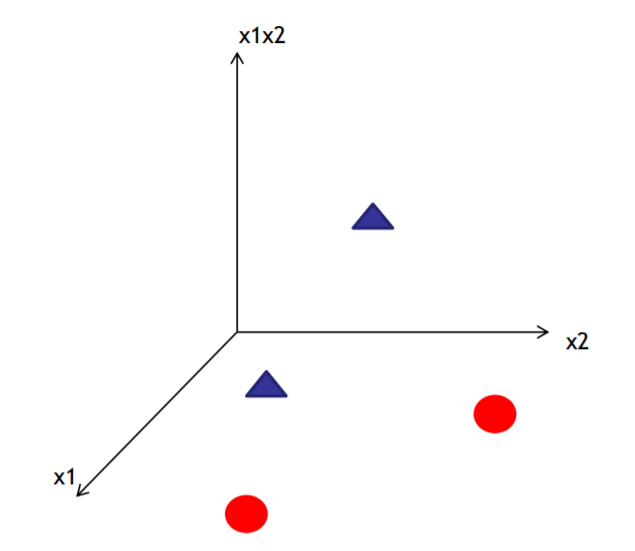
例子： 例如添加一个新维度 等于 X1*X2
object LogisticRegression3 {
def main(args: Array[String]) {
val conf = new SparkConf().setAppName("spark").setMaster("local[3]")
val sc = new SparkContext(conf)
// 解决线性不可分我们来升维,升维有代价,计算复杂度变大了
val inputData = MLUtils.loadLibSVMFile(sc, "./SparkMLlib/线性不可分数据集.txt")
.map { labelpoint =>
val label = labelpoint.label
val feature = labelpoint.features
val array = Array(feature(0), feature(1), feature(0) * feature(1)) // 增加维度 feature(0) * feature(1)
val convertFeature = Vectors.dense(array)
new LabeledPoint(label, convertFeature)
}
val splits = inputData.randomSplit(Array(0.7, 0.3))
val (trainingData, testData) = (splits(0), splits(1))
val lr = new LogisticRegressionWithLBFGS()
lr.setIntercept(true)
val model = lr.run(trainingData)
val result = testData.map { point => Math.abs(point.label - model.predict(point.features)) }
println("正确率=" + (1.0 - result.mean()))
println(model.weights.toArray.mkString(" "))
println(model.intercept)
}
}不增加维度的正确率为：
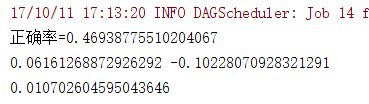
增加新维度正确率为：
梯度下降法：
上面讲了两种方法让 方程 在大的范围内确立了方程求解的可能性 ，
而其中一种方程求解方法 — 梯度下降法 是以更快的方法调整参数w使方程逼近最优解
SGD： 随机梯度下降法 LogisticRegressionWithSGD()
另外一种算法为 拟牛顿法 : LogisticRegressionWithLBFGS()
这里讲解随机梯度下降法：
首先： 
判断求出的参数是否为最优解是 计算有模型算出的预测值与正确值之间的误差 判断的
误差方程为： （不需要理解）
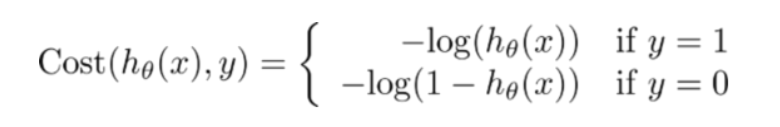
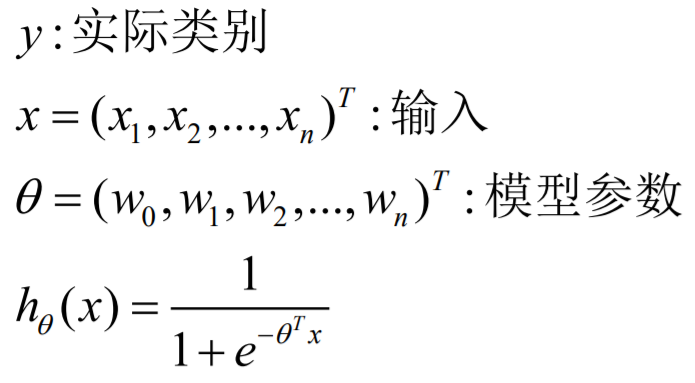
站在数学的角度上来说，即误差方程值最小化 即最优解：
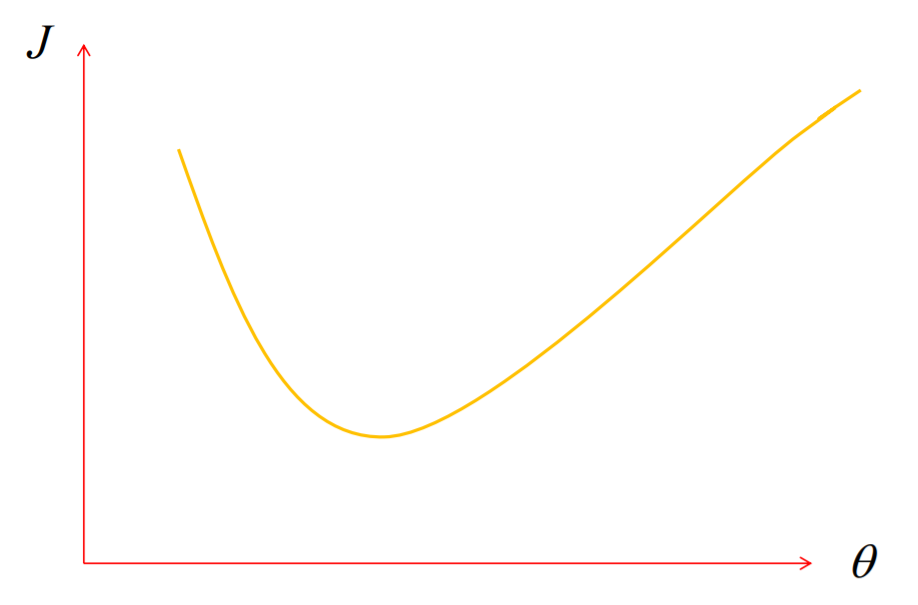
1、极值分为极大值和极小值
2、已经由数学证明上述误差函数为凹函数，即只有极小值，无极大值
3、因此求解最小值的过程就为求解极值的过程
对误差方程求导，求极值就是让导数等于0：
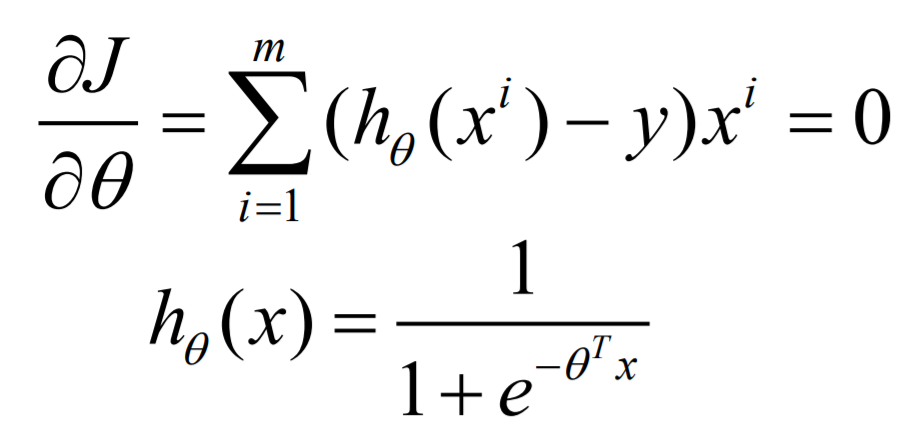
但是求解合适的参数很困难，可以看到几乎无法求解
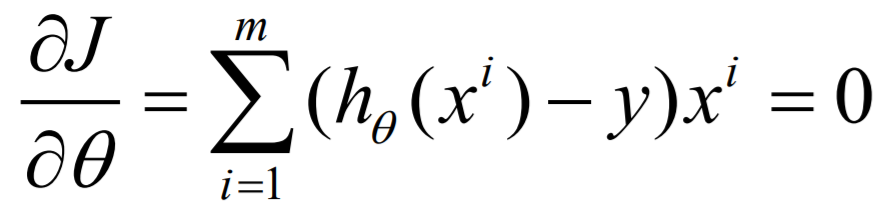
已知参数，代入公式计算结果却很容易：
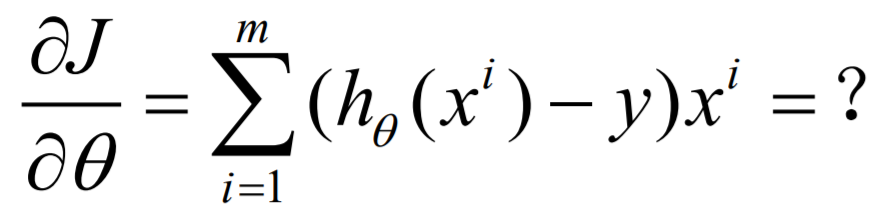
对于一组参数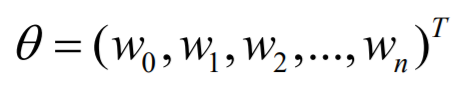 
对于多组参数：
可以看到 随着参数组的变化，误差值在慢慢减小，最终达到一个凹点即极小值 ，即如果误差减少就继续减小，如果变大就回退回去。
把误差函数当成一座山，梯度就是往前走时陡峭程度的数字化表现：
最优解是达到山底， 绝对值越大，此时山越陡峭
1、梯度 > 0,往前走是上山 ，往回走
2、梯度 < 0,往前走是下山，每次往下走一定的距离（Step步长），停下来再寻找另外一个坡度最陡（斜率最大）的方向往下走，
3、如此循环，直到谷底（斜率为0）。
公式：
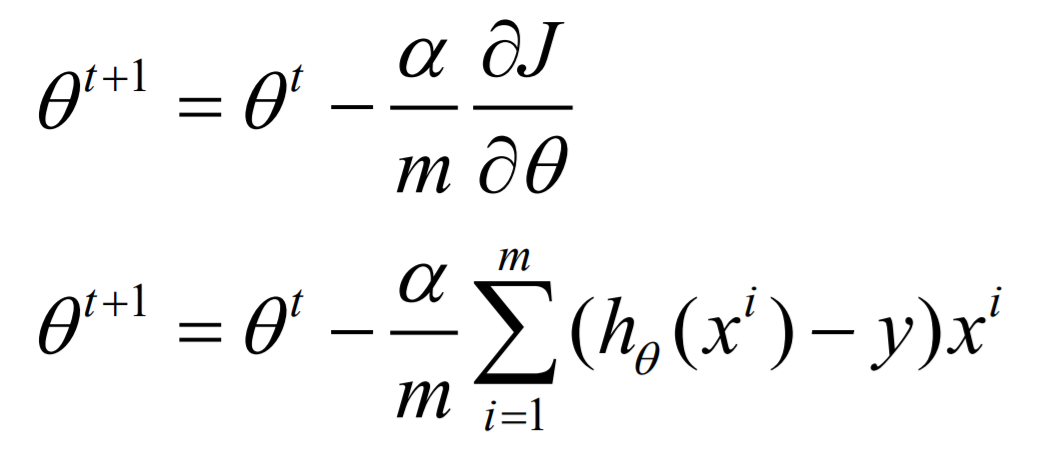
//逻辑回归训练，两个参数，迭代次数和步长，生产常用调整参数 val lr = new LogisticRegressionWithSGD() // 设置W0截距 lr.setIntercept(true) // 设置梯度下降的步长 lr.optimizer.setStepSize(0.1) // 最大迭代次数 lr.optimizer.setNumIterations(10) val model: LogisticRegressionModel = lr.run(la)