理解回归（regression）
回归问题：
一个唯一的 因变量(dependentvariable) ( 需要预测的值 ) 和 一个或多个数值型的 自变量(independent variables) ( 输入数据 )之间的关系。
回归即 预测：
根据现有的数据求出模型（根据数据求出方程组的系数）
预测未来（带入新数据，根据方程，求出Y）
广义线性回归：
GLM。比如，逻辑回归，泊松回归。
一元线性回归：
对于简单线性回归问题，也就是小学大家就都会了的解应用题。
Y = a + bx
求出 最优解 ： 线性回归最优解就是让不同的数据均匀的分布在线的两边
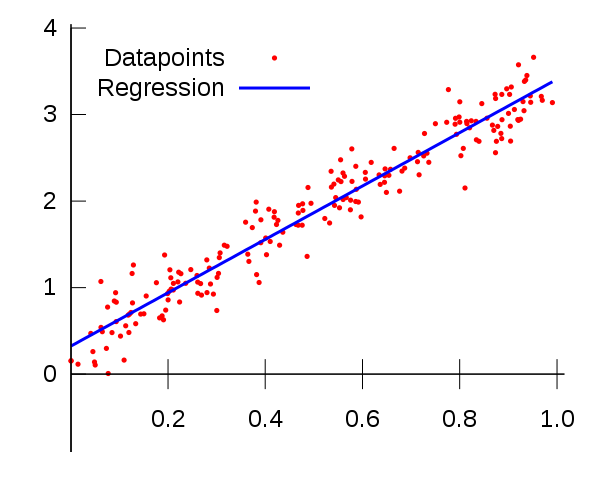
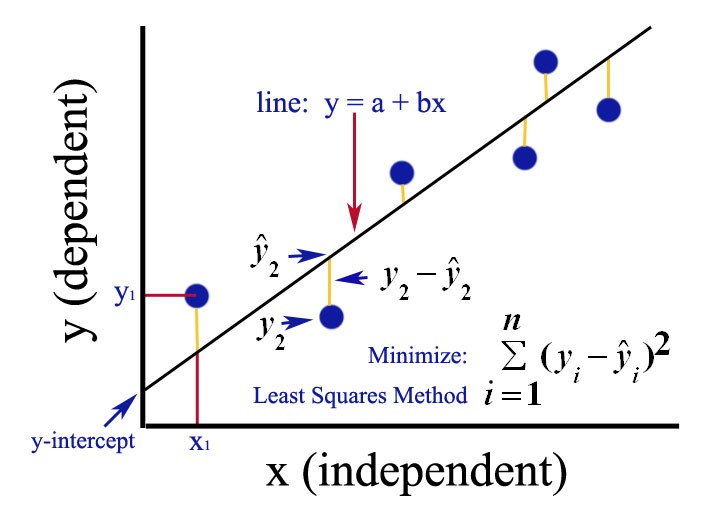
误差最小即最优解
—— 如何定义误差最小呢？
根据数据求出模型后，在带入数据里输入值，求得目标值，比较 原数据里的目标值 与 模型求出的目标值，可得 误差。
在分类或者回归任务中，便是使用 损失函数（Loss Function）作为求解的目标函数，又称为代价函数(Cost Function) 。
在分类或者回归任务中，便是使用 损失函数（Loss Function）作为求解的目标函数，又称为代价函数(Cost Function) 。
线性回归使用的损失函数是 最小二乘法，即对模型带入源数据得到相比源数据不同y，这其中的差值的平方和，就是误差值。
相关系数
• 两个变量之间的相关系数是一个数，它表示两个变量服从一条直线的关系有多么紧密。
即可以用来看 Y 和 某一个维度(x) 的相关程度，用来从不确定的维度中挑选合适的维度
• 相关系数（Pearson相关系数），它是数学家Pearson提出来的：
相关系数的范围是-1~+1之间，两端的值表示一个完美的线性关系
相关系数接近于0则表示不存在线性关系。
• 根据 协方差函数cov()、标准方差函数sd()，可以求出来 cor()
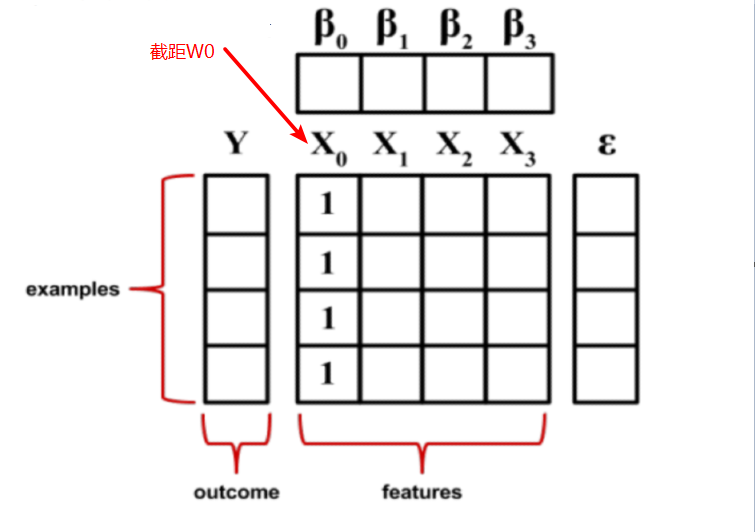多元线性回归 大多数现实世界的分析不止一个自变量，大多数情况下，很有可能使用多元线性回归
。
即预测一个值，需要从多个维度考虑。
公式：
y = w0 + w1*x1 + w2*x2 + w3*x3 + w4*x4
y = w0 + w1*x1 + w2*x2 + w3*x3 + w4*x4
求导：
求取参数w0、w1、w2、w3、w4的值
保险例子
保险公司根据
不同情况的客户的对应的医疗费，算出模型， 然后根据新客户提交的资料来预测该客户可能未来的医疗费来判断是否卖给该客户保险。
这个采用R语言求出模型
数据：
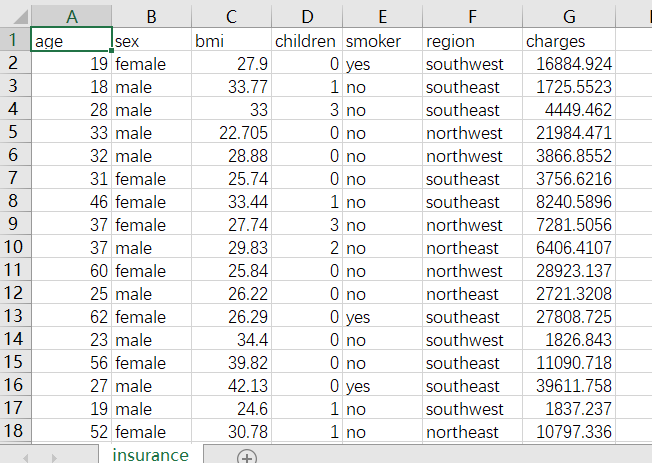
代码：
# read.csv
# 指定文件路径，为相对于工作目录的路径
# stringsAsFactors：是否把每个列中为string类型的作为Factor因子类型
# 例如：sex列中实际只有male和female两种值，
# 那就可以把sex列解析为Factor因子类型，有male和female两种因子
insurance <- read.csv("LinearRegression/data/insurance.csv", stringsAsFactors = TRUE)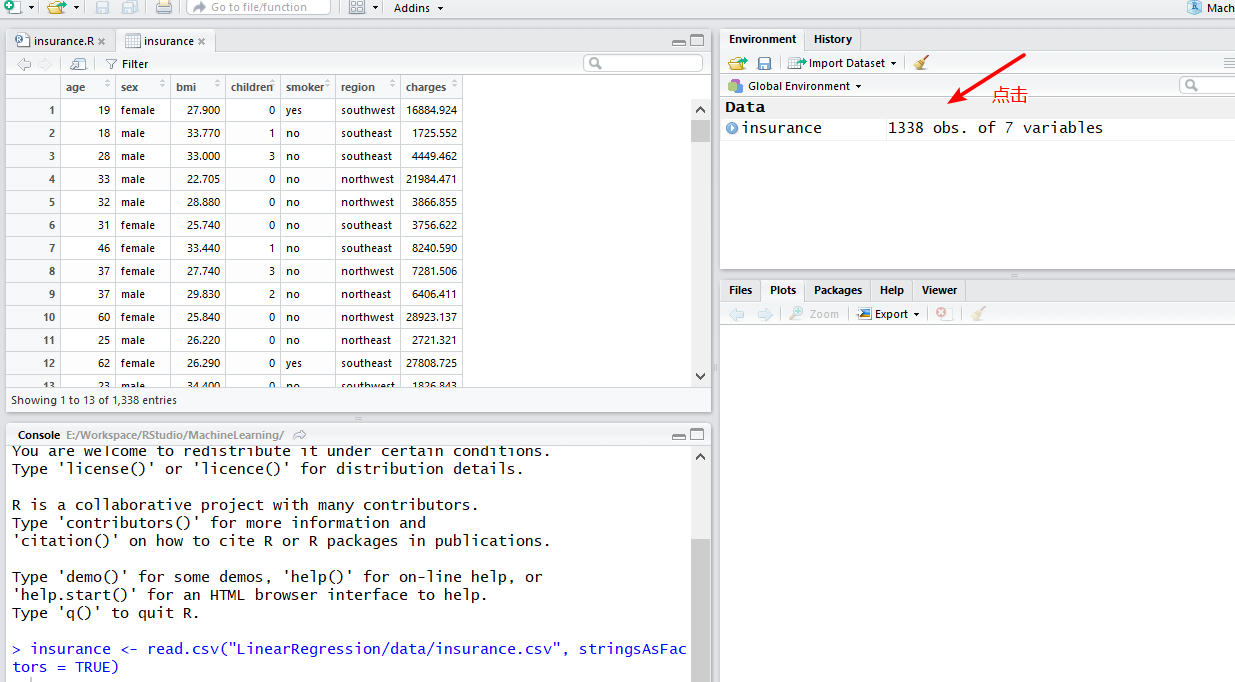
# 查看这张表 data.frame
# 可以看到sex、smoker、region为Factor类型
str(insurance)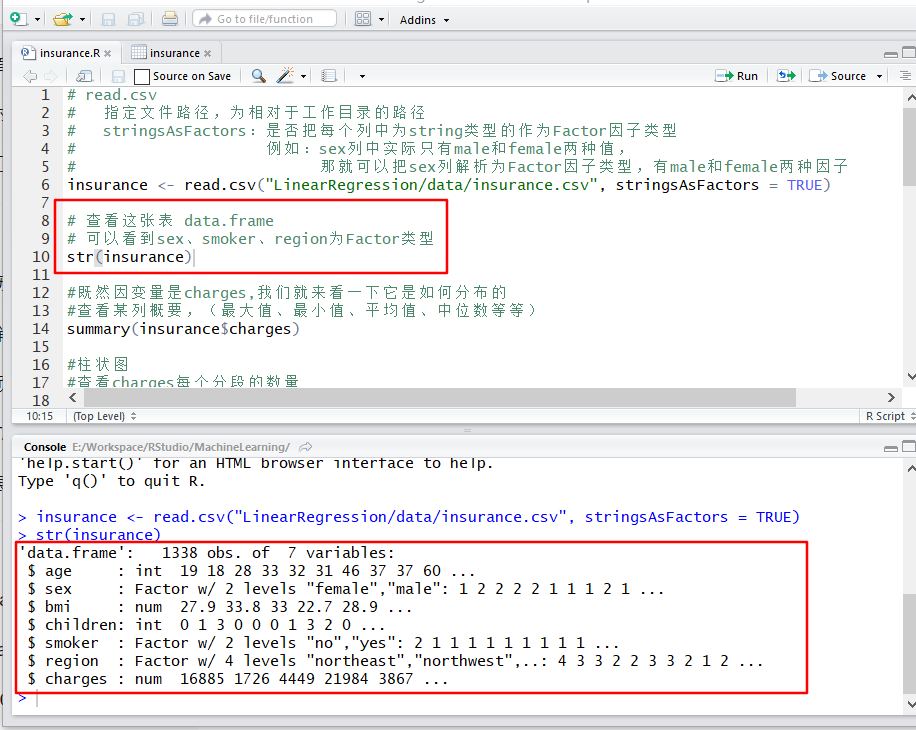
#既然因变量是charges,我们就来看一下它是如何分布的
#查看某列概要，（最大值、最小值、平均值、中位数等等）
summary(insurance$charges)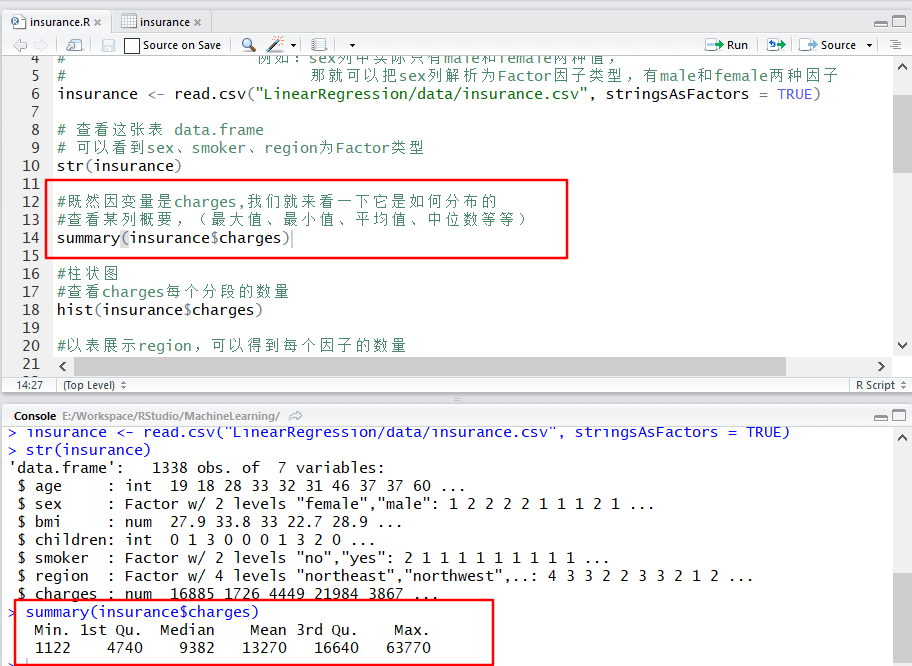
#柱状图
#查看charges每个分段的数量
hist(insurance$charges)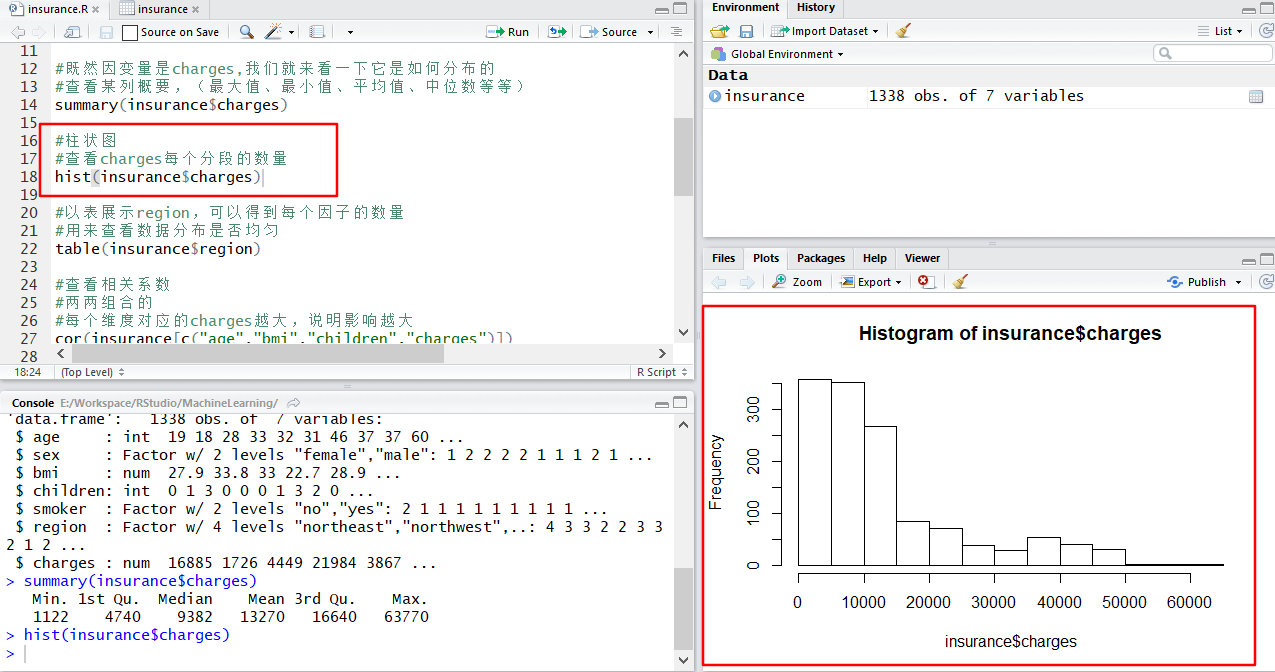
#以表展示region，可以得到每个因子的数量
#用来查看数据分布是否均匀
table(insurance$region)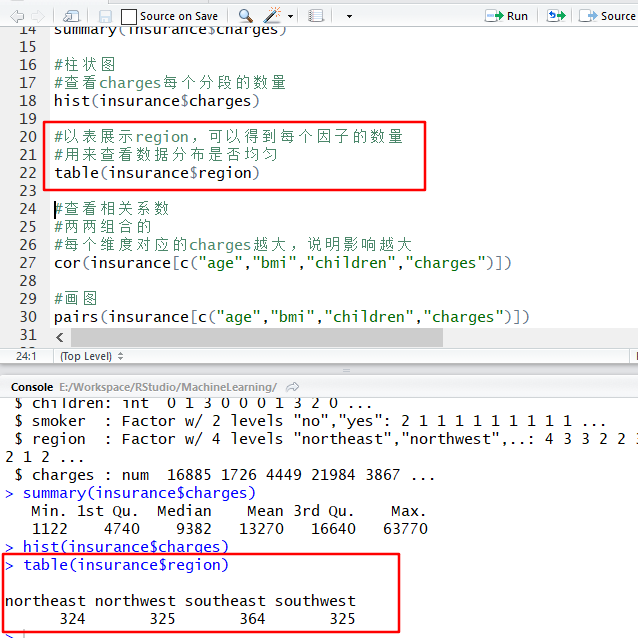
#查看相关系数
#两两组合的
#每个维度对应的charges越大，说明影响越大
cor(insurance[c("age","bmi","children","charges")])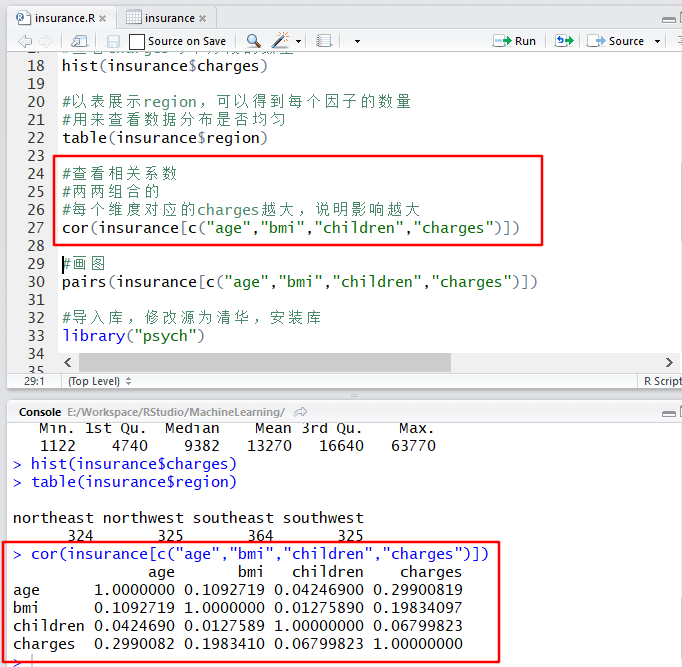
#画图
pairs(insurance[c("age","bmi","children","charges")])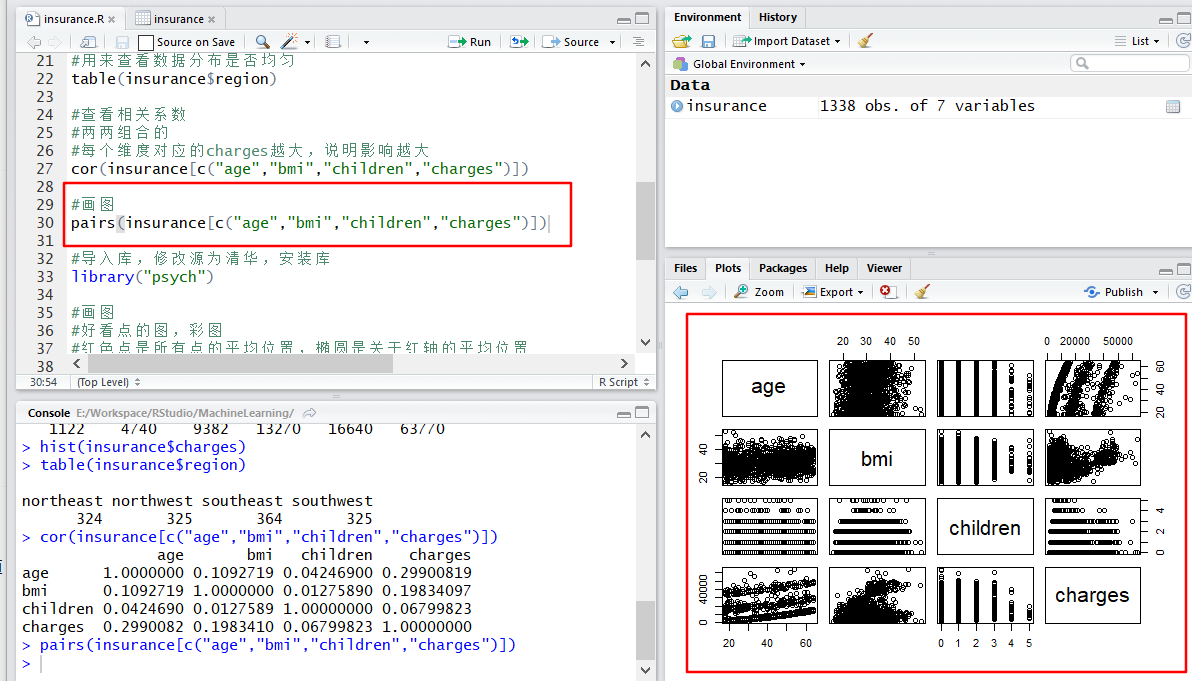
#导入库
#修改源为清华，安装psych库
library("psych")
#第二种方法导入在右下角点Packages标签，勾选psych即导入
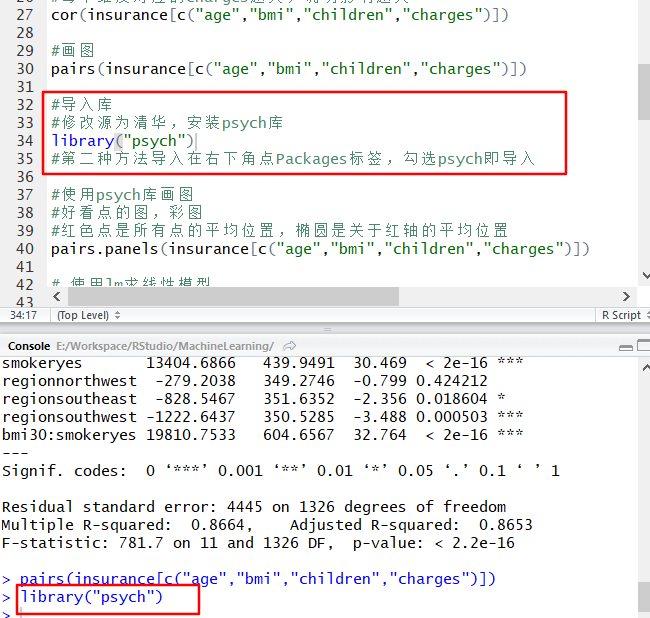
#使用psych库画图
#好看点的图，彩图
#红色点是所有点的平均位置，椭圆是关于红轴的平均位置
pairs.panels(insurance[c("age","bmi","children","charges")])
# 使用lm求线性模型
# 第一个参数为 因变量+ ~ + 作为维度的列
# 哪些列作为维度，由上面的分析和经验得出
# 第二个的参数为 数据对象
ins_model <- lm(charges ~ age + children + bmi + sex + smoker + region, data=insurance)
# 所有维度作为对象 可以用.代替
# ins_model <- lm(charges ~ . , data=insurance)#查看模型
#intercent：截距，数值是系数（权重）
#factor因子类别的话，会把一个维度拆成多个维度，只显示n-1个维度，剩下一个维度作为基准维度，值为0
# 例如：如果是两个因子的话，会只显示一个维度，默认把另外一个维度设置为0，显示的是基于0的相对值
ins_model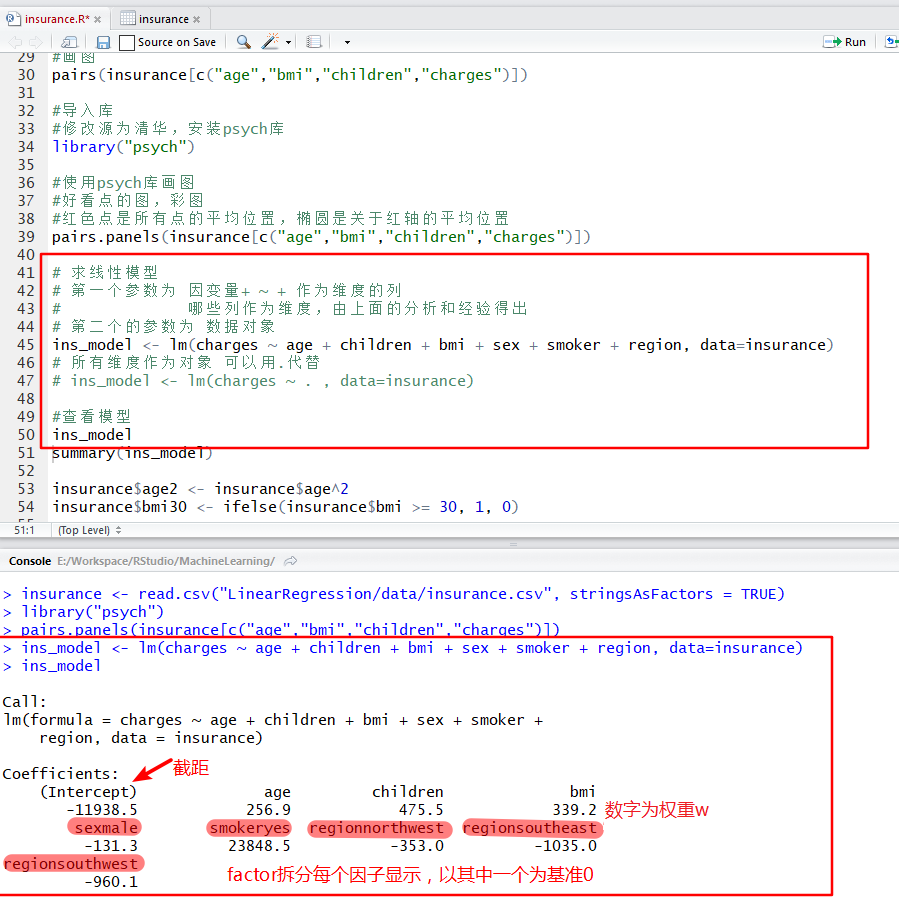
#模型概况
# Coefficients：查看每个维度对结果的影响，星越多越重要
# Residual standard error：误差值，误差值的平方和，越小越好
summary(ins_model)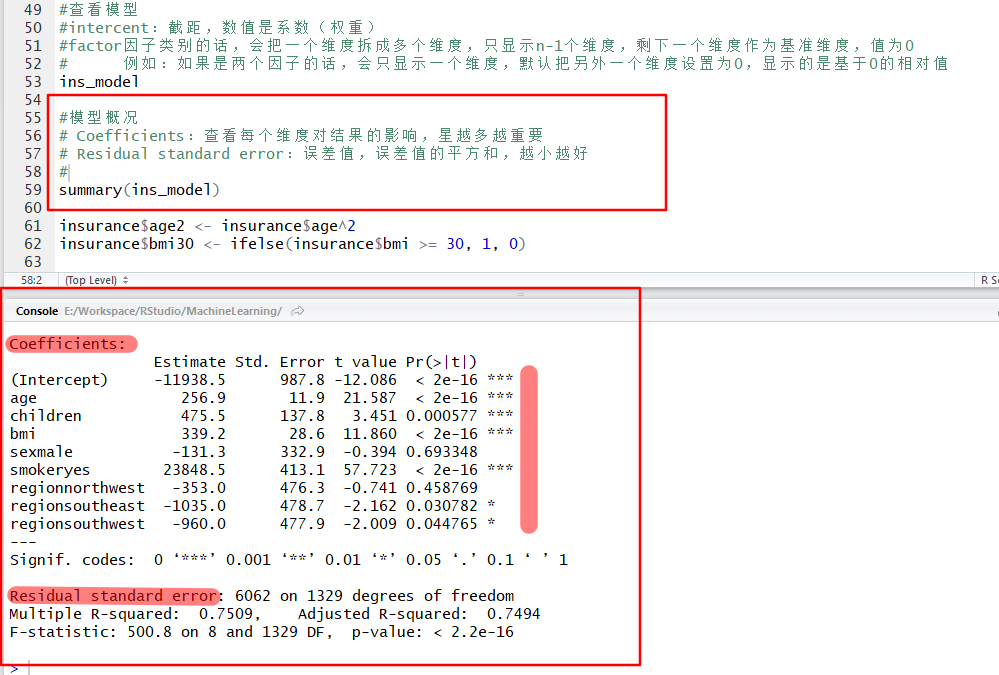 
#让age的平方作为新的一列
#多元线性回归，是要x与y的相关符合线性关系，这里是算法不变，让数据更加符合算法
# 如果x与y确实不是线性关系，y不可变，那就改变x的
# 例如将x平方，看能不能把 x与y的曲线拉直
insurance$age2 <- insurance$age^2
#构建新列 bmi大于30作为1，小于三十作为0
#类似归一化，减少bmi的情况
insurance$bmi30 <- ifelse(insurance$bmi >= 30, 1, 0)
#lm计算新模型
#bmi30*smoker：将两个维度合并为一个维度，例如即肥胖又抽烟
# 在你更了解业务的情况下，可以这样做
ins_models <- lm(charges ~ age + age2 + children + bmi + sex + bmi30*smoker + region , data=insurance)
#查看模型
#看误差值是否减小
summary(ins_models)
#误差值并不是越小越好，可能会过拟合，这个模型过于拟合这部分数据，并不适应于其他数据。
#解决办法：增加数据、修改算法、增加训练集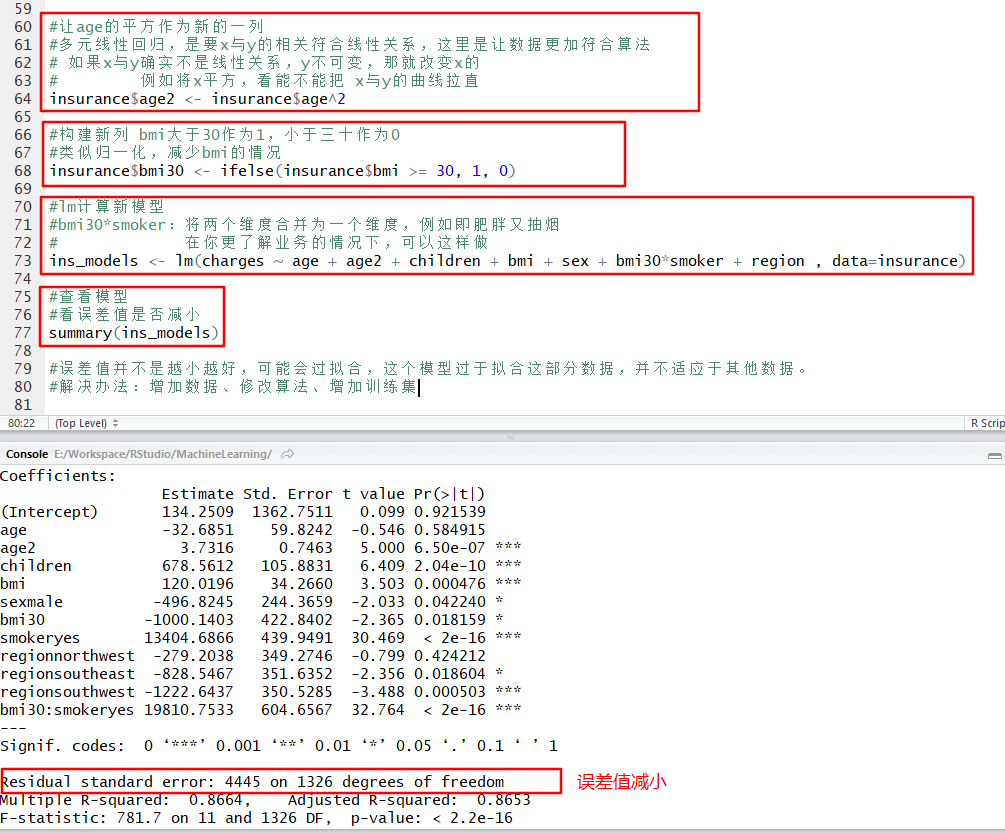
完整代码：
# read.csv
# 指定文件路径，为相对于工作目录的路径
# stringsAsFactors：是否把每个列中为string类型的作为Factor因子类型
# 例如：sex列中实际只有male和female两种值，
# 那就可以把sex列解析为Factor因子类型，有male和female两种因子
insurance <- read.csv("LinearRegression/data/insurance.csv", stringsAsFactors = TRUE)
# 查看这张表 data.frame
# 可以看到sex、smoker、region为Factor类型
str(insurance)
#既然因变量是charges,我们就来看一下它是如何分布的
#查看某列概要，（最大值、最小值、平均值、中位数等等）
summary(insurance$charges)
#柱状图
#查看charges每个分段的数量
hist(insurance$charges)
#以表展示region，可以得到每个因子的数量
#用来查看数据分布是否均匀
table(insurance$region)
#查看相关系数
#两两组合的
#每个维度对应的charges越大，说明影响越大
cor(insurance[c("age","bmi","children","charges")])
#画图
pairs(insurance[c("age","bmi","children","charges")])
#导入库
#修改源为清华，安装psych库
library("psych")
#第二种方法导入在右下角点Packages标签，勾选psych即导入
#使用psych库画图
#好看点的图，彩图
#红色点是所有点的平均位置，椭圆是关于红轴的平均位置
pairs.panels(insurance[c("age","bmi","children","charges")])
# 使用lm求线性模型
# 第一个参数为 因变量+ ~ + 作为维度的列
# 哪些列作为维度，由上面的分析和经验得出
# 第二个的参数为 数据对象
ins_model <- lm(charges ~ age + children + bmi + sex + smoker + region, data=insurance)
# 所有维度作为对象 可以用.代替
# ins_model <- lm(charges ~ . , data=insurance)
#查看模型
#intercent：截距，数值是系数（权重）
#factor因子类别的话，会把一个维度拆成多个维度，只显示n-1个维度，剩下一个维度作为基准维度，值为0
# 例如：如果是两个因子的话，会只显示一个维度，默认把另外一个维度设置为0，显示的是基于0的相对值
ins_model
#模型概况
# Coefficients：查看每个维度对结果的影响，星越多越重要
# Residual standard error：误差值，误差值的平方和，越小越好
summary(ins_model)
#让age的平方作为新的一列
#多元线性回归，是要x与y的相关符合线性关系，这里是算法不变，让数据更加符合算法
# 如果x与y确实不是线性关系，y不可变，那就改变x的
# 例如将x平方，看能不能把 x与y的曲线拉直
insurance$age2 <- insurance$age^2
#构建新列 bmi大于30作为1，小于三十作为0
#类似归一化，减少bmi的情况
insurance$bmi30 <- ifelse(insurance$bmi >= 30, 1, 0)
#lm计算新模型
#bmi30*smoker：将两个维度合并为一个维度，例如即肥胖又抽烟
# 在你更了解业务的情况下，可以这样做
ins_models <- lm(charges ~ age + age2 + children + bmi + sex + bmi30*smoker + region , data=insurance)
#查看模型
#看误差值是否减小
summary(ins_models)
#误差值并不是越小越好，可能会过拟合，这个模型过于拟合这部分数据，并不适应于其他数据。
#解决办法：增加数据、修改算法、增加训练集