GZIP
gzip是一个很老的算法了,在应用中也常使用到,以前学算法的时候学习了下,
就是对相同的内容,保存为一个内容,就是同样的内容可以用另外一个已经有的位置来替换。
最近有人问我:对gzip的处理都是流式的,例如 Java 中的 GZIPInputStream 和 GZIPOutputStream。那么 流式它是怎么实现压缩的 呢?
我就整理一下以前学习时写的文档,顺便写篇文章,好久都没写了(最近太懒了~)
“其实gzip的算法本身就是流式的”
gzip 对于要压缩的文件,首先对于要压缩的文件,首先使用 LZ77算法 的一个变种进行压缩,对得到的结果再使用 Huffman编码 的方法进行压缩。
所以明白了LZ77算法和Huffman编码的压缩原理,也就明白了gzip的压缩原理。我们来对LZ77算法和Huffman编码做一个简单说明:
一、LZ77算法简介
这一算法是由 Jacob Ziv 和 Abraham Lempel 于 1977 年提出,所以命名为 LZ77。
(1)、压缩原理
如果文件中有两块内容相同的话,那么只要知道前一块的位置和大小,我们就可以确定后一块的内容。
所以我们可以用(两者之间的距离,相同内容的长度 )这样一对信息,来替换后一块内容。
由于(两者之间的距离,相同内容的长度 )这一对信息的占用空间,小于被替换内容的占用空间,所以文件得到了压缩。
下面我们来举一个例子,有一个文件的内容如下:
湖南长沙岳麓山小学 湖南长沙宁乡小学
其中有些部分的内容,前面已经出现过了,下面用 () 括起来的部分就是相同的部分。
湖南长沙岳麓山小学 (湖南长沙)宁乡(小学)
我们使用 (两者之间的距离,相同内容的长度 ) 这样一对信息,来替换后一块内容。
湖南长沙岳麓山小学 (10,4)宁乡(9,2)
(10,4)中,10为相同内容块与当前位置之间的距离,4为相同内容的长度。
(9,2)中,9为相同内容块与当前位置之间的距离,2为相同内容的长度。
由于(两者之间的距离,相同内容的长度)这一对信息的大小,小于被替换内容的大小,所以文件得到了压缩。
(2)、实现过程:
1、使用滑动窗口寻找匹配串
LZ77算法使用"滑动窗口"的方法,来寻找文件中的相同部分:也就是匹配串。
我们先对这里的串做一个说明:
它是指一个任意字节的序列,而不仅仅是可以在文本文件中显示出来的那些字节的序列。
这里的串强调的是它在文件中的位置,它的长度随着匹配的情况而变化。
LZ77从文件的开始处开始,一个字节一个字节的向后进行处理一个固定大小的窗口,随着处理的字节不断的向后滑动。
对于文件中的每个字节,用 当前处理字节开始的串,和 窗口中的每个串进行匹配 ,寻找最长的匹配串。
窗口中的每个串指,窗口中每个字节开始的串
如果当前处理字节开始的串在 窗口中有匹配串,就用(之间的距离,匹配长度 ) 这样一对信息,来替换当前串,
处理文件中第一个字节的时候,窗口在当前处理字节之前,也就是还没有滑到文件上,这时窗口中没有任何内容,被处理的字节就会不做改动的输出。
如果当前处理字节开始的串在 窗口中没有匹配串,就不做改动的输出当前处理字节。
然后从刚才处理完的串之后的下一个字节,继续处理。
随着处理的不断向后,窗口越来越多的滑入文件,最后整个窗口滑入文件,然后整个窗口在文件上向后滑动,直到整个文件结束。
具体一个串在一个窗口内是怎么匹配最大长度的,文字不好描述,看下图:


2、规则:
为了在解压缩时,可以区分 “没有匹配的字节 ” 和 “(之间的距离,匹配长度 ) 对 ”:
我们还需要在每个“没有匹配的字节”或者“(之间的距离,匹配长度)对”之前,放上一位,来指明是“没有匹配的字节”,还是“(之间的距离,匹配长度)对”。
我们用 0 表示“没有匹配的字节”,用 1 表示“(之间的距离,匹配长度)对”。
实际中,我们将固定 (之间的距离,匹配长度 ) 对中的 “之间的距离” 和 “匹配长度” 所使用的 位数 :
由于我们要固定 “之间的距离” 所使用的位数,所以我们才使用了 固定大小的窗口,
比如窗口的大小为32KB,那么用15位(2^15=32K)就可以保存0-32K范围的任何一个值。
实际中,我们还将限定 最大的匹配长度 ,这样一来,“匹配长度” 所使用的位数也就固定了。
实际中,我们还将设定一个 最小匹配长度 :
只有当两个串的匹配长度大于最小匹配长度时,我们才认为是一个匹配。
举一个例子来说明这样做的原因:
比如,“距离”使用15位,“长度”使用8位,那么“(之间的距离,匹配长度)对”将使用23位,也就是差1位3个字节。
如果匹配长度小于3个字节的话,那么用“(之间的距离,匹配长度)对”进行替换的话,不但没有压缩,反而会增大,
所以需要一个最小匹配长度。
(3)、压缩和解压缩:
压缩:
- 从文件的开始到文件结束,一个字节一个字节的向后进行处理。用当前处理字节开始的串,和滑动窗口中的每个串进行匹配,寻找最长的匹配串。
- 如果当前处理字节开始的串在窗口中有匹配串,就先输出一个标志位,表明下面是一个(之间的距离,匹配长度) 对,然后输出(之间的距离,匹配长度) 对,然后从刚才处理完的串之后的下一个字节,继续处理。
- 如果当前处理字节开始的串在窗口中没有匹配串,就先输出一个标志位,表明下面是一个没有改动的字节,然后不做改动的输出当前处理字节,
- 然后继续处理当前处理字节的下一个字节。
解压缩:
- 从文件开始到文件结束,每次 先读一位标志位 ,通过这个标志位来 判下面是 一个(之间的距离,匹配长度) 对 ,还是 一个没有改动的字节。
- 如果是 一个(之间的距离,匹配长度) 对,就 读出固定位数的(之间的距离,匹配长度)对,然后根据对中的信息,将匹配串输出到当前位置。
- 如果是 一个没有改动的字节,就读出一个字节,然后输出这个字节。
可以看到,LZ77压缩时需要做大量的匹配工作,而解压缩时需要做的工作很少,也就是说解压缩相对于压缩将快的多。
这对于需要进行一次压缩,多次解压缩的情况,是一个巨大的优点。
二、Huffman编码简介
(1)压缩原理
我们把文件中的字符用 变长的值 表示,比如把8位长的256种值,也就是字节的256种值看作是符号。
我们根据这些 符号在文件中出现的频率,对 这些符号重新编码 。
对于出现次数非常多 的,我们 用较少的位数 来表示,对于 出现次数非常少 的,我们用较多的位数 来表示。
这样一来,文件的一些部分位数变少了,一些部分位数变多了,
由于变小的部分比变大的部分多,所以整个文件的大小还是会减小,所以文件得到了压缩。
1、使用Huffman树来产生编码
要进行Huffman编码,首先要把整个文件读一遍,在读的过程中,统计每个符号(我们把字节的256种值看作是256种符号)的出现次数。
然后根据符号的出现次数,建立Huffman树,通过Huffman树得到每个符号的新的编码。
对于文件中出现次数较多的符号,它的Huffman编码的位数比较少。
对于文件中出现次数较少的符号,它的Huffman编码的位数比较多。
然后把文件中的每个字节替换成他们新的编码 。
2、建立Huffman树:
首先把 所有符号 看成是 只有一个结点的树,并且 该结点的值为它的出现次数。
每次从所有树中找出 值最小的两个树,为这两个树 建立一个父结点 ,然后这两个树和它们的父结点组成一个新的树,这个新的树的值为它的两个子树的值的和。
然后再 重新找值最小的两个树 ,而刚刚新建的树中的父节点则代表该树的值
如此往复,直到最后所有的树变成了一棵树。我们就 得到了一棵Huffman树,而所有的符号在该树叶子节点上。
3、通过Huffman树得到Huffman编码:
这棵Huffman树,是一棵二叉树,它的 所有叶子结点就是所有的符号,它的中间结点是在产生Huffman树的过程中不断建立的。
我们在Huffman树的所有父结点到它的 左子结点的路径上标上0,右子结点的路径上标上1。
现在我们从 根节点开始,到所有叶子结点的路径,就是一个0和1的序列。用这个序列,作为这个叶子结点的Huffman编码。
4、我们来看一个例子。
有一个文件的内容如下
abbbbccccddde
我们统计一下各个符号的出现次数,
a b c d e
1 4 4 3 1
根据次数建立Huffman树的过程如图:
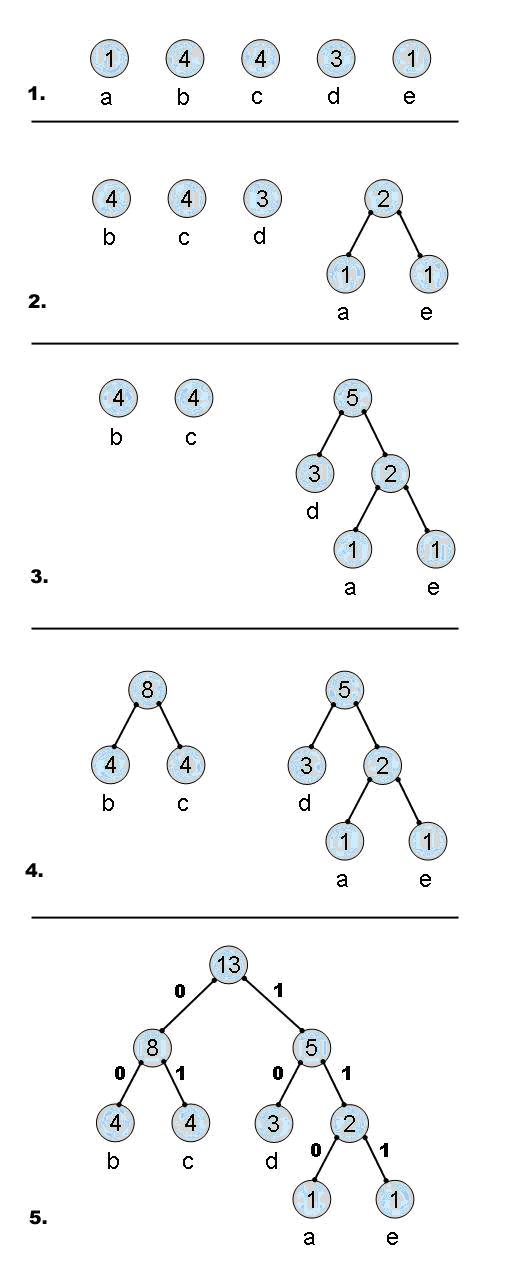
通过最终的Huffman树,我们可以得到每个符号的Huffman编码。
a 为 110
b 为 00
c 为 01
d 为 10
e 为 111
我们可以看到,Huffman树的建立方法就保证了:
出现次数多的符号,得到的Huffman编码位数少,
出现次数少的符号,得到的Huffman编码位数多。
各个符号的Huffman编码的长度不一,也就是变长编码:
对于变长编码,可能会遇到一个问题,就是重新编码的文件中可能会 无法区分这些编码。
比如,a的编码为000,b的编码为0001,c的编码为1,那么当遇到0001时,就不知道0001代表ac,还是代表b。
出现这种问题的原因是a的编码是b的编码的前缀。
由于Huffman编码为根结点到叶子结点路径上的0和1的序列,也就是说 所有符号都是叶子,而一个叶子结点的路径不可能是另一个叶子结点路径的前缀,
所以一个Huffman编码不可能为另一个Huffman编码的前缀,这就保证了Huffman编码是可以区分的。
(2)、压缩和解压缩:
为了在解压缩的时候,得到压缩时所使用的Huffman树,我们需要在 压缩文件中,保存树的信息,也就是保存每个符号的出现次数的信息。
压缩:
- 读文件,统计每个符号的出现次数。根据 每个符号的出现次数 ,建立Huffman树,得到每个符号的Huffman编码。
- 将每个符号的 出现次数的信息保存在压缩文件 中,
- 将文件中的 每个符号替换成它的Huffman编码 ,并输出。
解压缩:
- 得到 保存在压缩文件中的,每个符号的出现次数的信息。
- 根据 每个符号的出现次数,建立Huffman树,得到每个符号的Huffman编码。
- 将压缩文件中的 每个Huffman编码替换成它对应的符号 ,并输出。
对于其他细节以后再总结,例如
为一个串寻找匹配串需要进行大量的匹配工作,而且还需要为很多很多个串寻找匹配串。
所以 gzip 在寻找匹配串的实现中使用哈希表来提高速度。